Page 33 - 2024年第55卷第12期

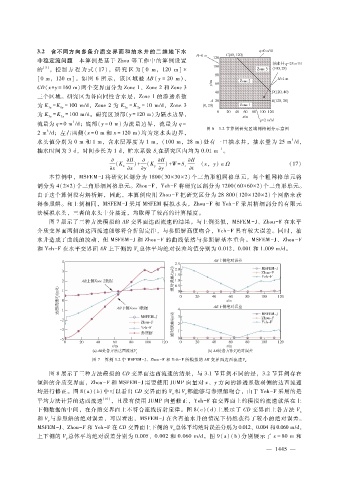
３．２ 含不同方向多条介质交界面和抽水井的二维地下水
非稳定流问题 本算例是基于 Ｚｈｏｕ等工作中的算例设置
的 ［５］ ，控制 方 程 为 式 （１７）， 研 究 区 为 ［０ｍ，１２０ｍ］ ×
［０ｍ，１２０ｍ］。如 图 ６所 示，该 区 域 被 ＡＢ（ｙ ＝２０ｍ）、
ＣＤ（ｘ ＋ ｙ ＝ １６０ｍ ）两个交界面分为 Ｚｏｎｅ１、Ｚｏｎｅ２和 Ｚｏｎｅ３
三个区域。研究区为各向同性含水层，Ｚｏｎｅ１的渗透系数
为 Ｋ ＝ Ｋ ＝ １００ｍ?ｄ ，Ｚｏｎｅ２为 Ｋ ＝ Ｋ ＝ １０ｍ?ｄ ，Ｚｏｎｅ３
２ｘ
１ｘ
２ｙ
１ｙ
为 Ｋ ＝ Ｋ ＝ １００ｍ?ｄ 。研究区顶部（ｙ ＝ １２０ｍ ）为隔水边界，
３ｘ ３ｙ
３
流量为 ｑ ＝ ０ｍ ?ｄ；底部（ｙ ＝ ０ｍ）为流量边界，流量为 ｑ ＝
图 ６ ３．２节算例研究区域网格剖分示意图
３
２ｍ ?ｄ；左右两侧（ｘ ＝ ０ｍ和 ｘ ＝ １２０ｍ ）均为定水头边界，
３
水头值分别为 ０ｍ和 １ｍ，含水层厚度为 １ｍ，（１００ｍ，２８ｍ）处有一口抽水井，抽水量为 ２５ｍ ?ｄ，
－ １
抽水时间为 ３ｄ，时间步长为 １ｄ，贮水系数 Ｓ在研究区内均为 ０．０１ｍ 。
ｓ
  Ｈ   Ｈ  Ｈ
（Ｋ ） ＋ （Ｋ ） ＋ Ｗ＝ Ｓ （ｘ，ｙ） ∈Ω （１７）
 ｘ ｘ  ｘ  ｙ ｙ  ｙ ｓ  ｔ
本算例中，ＭＳＦＥＭ－ Ｊ将研究区划分为 １８００（３０ × ３０ × ２）个三角形粗网格单元，每个粗网格单元将
剖分为 ４（２ × ２）个三角形细网格单元。Ｚｈｏｕ － Ｆ、Ｙｅｈ － Ｆ将研究区剖分为 ７２００（６０ × ６０ × ２）个三角形单元。
由于这个算例没有解析解，因此，本算例应用 Ｚｈｏｕ － Ｆ把研究区分为 ２８８００（１２０ × １２０ × ２）个网格来获
得参照解。和上例相同，ＭＳＦＥＭ－ Ｊ采用 ＭＳＦＥＭ模拟水头，Ｚｈｏｕ － Ｆ和 Ｙｅｈ － Ｆ采用精细剖分的有限元
法模拟水头，三者的水头十分接近，均取得了较高的计算精度。
图 ７展示了三种方法模拟的 ＡＢ交界面达西流速的结果。与上例类似，ＭＳＦＥＭ－ Ｊ、Ｚｈｏｕ － Ｆ在水平
介质交界面两侧的达西流速能够符合折射定律，与参照解高度吻合，Ｙｅｈ － Ｆ具有较大误差。同时，抽
水井造成了曲线的波动，但 ＭＳＦＥＭ－ Ｊ和 Ｚｈｏｕ － Ｆ的曲线依然与参照解基本重合。ＭＳＦＥＭ－ Ｊ、Ｚｈｏｕ － Ｆ
和 Ｙｅｈ － Ｆ在水平交界面 ＡＢ上下侧的 Ｖ总体平均绝对误差均值分别为 ０．０１２、０．００１和 １．００９ｍ?ｄ。
ｘ

图 ７ 算例 ３．２中 ＭＳＦＥＭ－ Ｊ、Ｚｈｏｕ － Ｆ和 Ｙｅｈ － Ｆ所模拟的 ＡＢ交界面达西流速Ｖ ｘ
图 ８展示了三种方法模拟的 ＣＤ交界面达西流速的结果，与 ３．１节算例不同的是，３．２节算例存在
倾斜的介质交界面，Ｚｈｏｕ － Ｆ和 ＭＳＦＥＭ－ Ｊ需要使用 ＪＵＭＰ向量对 ｘ、ｙ方向的渗透系数弱侧的达西流速
均进行修正。图 ８（ａ）（ｂ）中可以看出 ＣＤ交界面的 Ｖ和 Ｖ都能够与参照解吻合，由于 Ｙｅｈ － Ｆ采用的是
ｘ ｙ
平均方法计算的达西流速 ［１０］ ，且没有使用 ＪＵＭＰ向量修正，Ｙｅｈ － Ｆ在交界面上的模拟的流速就落在上
下侧数据的中间，在介质交界面上不符合流线折射定律。图 ８（ｃ）（ｄ）上展示了 ＣＤ交界面上各方法 Ｖ
ｘ
和 Ｖ与参照解的绝对误差，可以看出，ＭＳＦＥＭ－ Ｊ在含有抽水井的情况下仍然获得了较小的绝对误差。
ｙ
ＭＳＦＥＭ － Ｊ、Ｚｈｏｕ － Ｆ和 Ｙｅｈ － Ｆ在 ＣＤ交界面上下侧的 Ｖ总体平均绝对误差分别为 ０．０１２、０．００４和 ０．０６０ｍ?ｄ，
ｘ
上下侧的 Ｖ总体平均绝对误差分别为 ０．００５、０．００２和 ０．０６０ｍ?ｄ。图 ９（ａ）（ｂ）分别展示了 ｘ ＝ ８０ｍ和
ｙ
— １ ４ ５ —
４