Page 51 - 2024年第55卷第12期

＋
粗糙度函数 ｆ并不是关于 Ｋ 的单一函数，基于文献［２６ － ２７］中粗糙度函数：
ｒ ｓ ＋
[ Ｋ － ２ ．２５ ｓ ｓ] ＋
ｓ
＋
ｆ ＝ ＋ ＣＫ × ｓｉｎ ｛０．４２５８（ｌｎＫ － ０ ．８１１）｝ （３）
ｒ ８７ ．７５ ｓ
１
将式（ ３）代入式 Δ Ｂ ＝ ｌｎｆ，可得
ｒ
κ
＋
ｓ ｓ]
１ Ｋ － ２．２５ ＋
ｓ
＋
Δ Ｂ ＝ ｌｎ [ { ＋ ＣＫ × ｓｉｎ ［０．４２５８（ｌｎＫ － ０ ．８１１）］ } （４）
ｓ
κ ８７ ．７５
式中，Ｃ为粗糙度常数，经对比本文研究结果与现有实验数据，对于混凝土壁面，推荐采用 Ｃ ＝ ０．６４
ｓ
ｓ
（Ｃ在 ０．５～１．０之间）。综上得到了考虑混凝土壁面粗糙度的改进壁面函数模型
ｓ
＋
( ) {
１ ρ ＾ｕｙ １ Ｋ － ２．２５
＋
＋ Ｐ ｓ ｓ ｓ] ＋
ｕ ＝ ｌｎＥ － ｌｎ [ ＋ ＣＫ × ｓｉｎ ［０．４２５８（ｌｎＫ － ０ ．８１１）］ } （５）
ｓ
κ μ κ ８７．７５
２．２ 计算域网格划分与数值模型验证
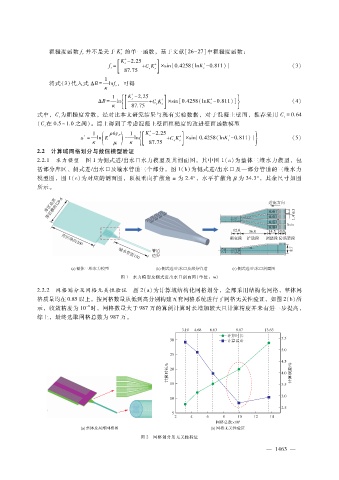
２．２．１ 水力模型 图 １为侧式进?出水口水力模型及其剖面图。其中图 １（ａ）为整体三维水力模型，包
括部分库区、侧式进?出水口及输水管道三个部分。图 １（ｂ）为侧式进?出水口及一部分管道的三维水力
模型图，图 １（ｃ）为对应的剖面图，顶板垂向扩散角 α为 ２．４°，水平扩散角 β 为 ３４．３°，其余尺寸如图
所示。

图 １ 水力模型及侧式进出水口剖面图（单位：ｍ）

２．２．２ 网格划分及网格无关性验证 图 ２（ａ）为计算域结构化网格划分，全部采用结构化网格，整体网
格质量均在 ０．８５以上。按网格数量从低到高分别构建五套网格系统进行了网格无关性验证，如图 ２（ｂ）所
－ ８
示，收敛精度为 １０ 时，网格数量大于 ９８７万的算例计算时长增加较大且计算精度并未有进一步提高，
综上，最终选取网格总数为 ９８７万。

图 ２ 网格划分及无关性验证

４
— １ ６ ３ —