Page 76 - 2025年第56卷第8期

é ê ê ù ú ú 0.62
ê (0.0022 + S v )V 3 h ú ú
ê
S * = 2.5 ê ê γ s - γ m ( 6D 50) ú ú （7）
ln
ê ú ú
ê κ m ghω s
ë γ m û
(
γ
γ m = γ + 1 - γ s) S （8）
N ( κ m V *) （9）
1
ω s
exp 8.21
a * =
( ) é ù
1 g ê ê 1 ú ú
ω s
ú ú
ê ê
N = ∫ 0 f c n C ，η exp 5.33 κ m V * arctg η - 1 dη （10）
( ) g g
û
ë
g
f c n C ，η = 1 - 3π + 8c n C ( η - η 2 + arcsin η ) （11）
8c n C
V g
V * = （12）
C
S v( 0.365 - S v)
c n = 0.15 - 0.63 （13）
é
ê ê( d 50) 3.5 ù ú ú
κ m = κ 0 1 - 4.2 S v( 0.365 - S v) ù û （14）
ë
é
ê ê
ê ê
ω s = ω 0 1 - S V ( 1 - 1.25S v) ú ú ú ú （15）
ë 2.25 û
式中：S 为体积百分比表示的含沙量，含沙量 S 与体积含沙量的关系为 S = γ s S v ；κ m 和 κ 0 分别为浑水、
v
清水卡门常数，κ 0 取 0.4；γ m 为浑水容重；ω 0 分别为泥沙在清水中的沉速；V * 为摩阻流速；C 为谢才系
数；d 为悬沙中值粒径。
50
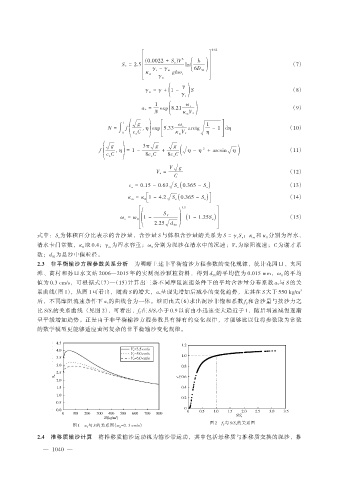
2.3 非平衡输沙方程参数关系分析 为明晰上述非平衡输沙方程参数的变化规律，统计花园口、夹河
滩、高村和孙口水文站 2006—2015 年的实测泥沙颗粒资料，得到 d 的平均值为 0.015 mm，ω 0 的平均
50
值为 0.3 cm/s，可根据式（7）—（15）计算出三条不同摩阻流速条件下的平均含沙量分布系数 a 与 S 的关
*
3
系曲线（图 1），从图 1 可看出，随着 S 的增大，a 呈现先增加后减小的变化趋势，尤其在 S 大于 550 kg/m
*
后，不同摩阻流速条件下 a 的曲线合为一体。继而由式（6）求出泥沙非饱和系数 f 和含沙量与挟沙力之
*
S
比 S/S 的关系曲线 （见图 2），可看出，f 在 S/S 小于 0.9 以前由小迅速变大趋近于 1，随后增速减慢逐渐
*
S
*
呈平缓增加趋势。正是由于非平衡输沙方程参数具有特有的变化规律，才能够比以往将参数取为常数
的数学模型更能够适应黄河复杂的非平衡输沙变化规律。

图 2 f 与 S/S 的关系图
图 1 a 与 S 的关系图（ω =0. 3 cm/s） S *
* 0
2.4 推移质输沙计算 将推移质输沙运动视为输沙带运动，其中包括悬移质与推移质交换的泥沙，推

— 1040 —