Page 146 - 2025年第56卷第9期

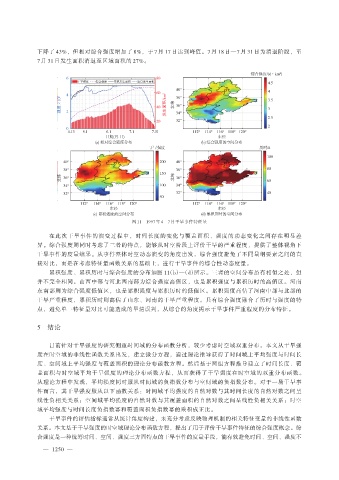
下降了 43%，但相对综合强度增加了 8%，于 7 月 17 日达到峰值。7 月 18 日—7 月 31 日为消退阶段，至
7 月 31 日发生面积消退至区域面积的 27%。

图 11 1997 年 4—7 月干旱事件特征量

在此次干旱事件的演变过程中，时间长度的变化与覆盖面积、强度的动态变化之间存在明显差
异。综合强度则同时考虑了三者的特点，能够从时空阶段上评价干旱的严重程度，提供了整体视角下
干旱事件的度量结果。从事件整体时空动态演变的角度出发，综合强度避免了不同量纲要素之间的直
接对比，而是在考虑特征量函数关系的基础上，进行干旱事件的综合性动态度量。
累积强度、累积历时与综合强度的分布如图 11（b）—（d）所示。三者的空间分布虽有相似之处，但
并不完全相同。山西中部与河北西南部为综合强度高值区，也是累积强度与累积历时的高值区。河南
东南部则为综合强度低值区，也是累积强度与累积历时的低值区。累积强度高估了河南中部与北部的
干旱严重程度，累积历时则高估了山东、河南的干旱严重程度。只有综合强度融合了历时与强度的特
点，避免单一特征量对比可能造成的旱情误判，从综合的角度揭示干旱事件严重程度的分布特征。

5 结论

目前针对干旱强度的研究侧重时间域的分布函数分析，较少考虑时空域双重分布。本文从干旱强
度在时空域的非线性函数关系出发，建立微分方程，通过理论推导获得了时间域上平均强度与时间长
度、空间域上平均强度与覆盖面积的理论分布函数方程。然后基于两组方程推导建立了时间长度、覆
盖面积与时空域平均干旱强度的理论分布函数方程，从而获得了干旱强度在时空域的双重分布函数。
从理论方程中发现，平均强度同时服从时间域的负指数分布与空间域的负指数分布。对于一场干旱事
件而言，其干旱强度服从以下函数关系：时间域平均强度的自然对数与其时间长度的自然对数之间呈
线性负相关关系；空间域平均强度的自然对数与其覆盖面积的自然对数之间呈线性负相关关系；时空
域平均强度与时间长度负指数幂和覆盖面积负指数幂的乘积成正比。
干旱事件的评估指标通常从统计角度构建，未充分考虑反映物理机制的相关特征变量的非线性函数
关系。本文基于干旱强度的时空域理论分布函数方程，提出了用于评价干旱事件特征的综合强度概念。综
合强度是一种统筹时间、空间、强度三方面特点的干旱事件的度量手段，能有效避免时间、空间、强度不

— 1250 —