Page 142 - 2025年第56卷第9期
P. 142
的干扰,采用以下规则来识别日尺度的干旱事件:
规则 1:在时间尺度上,干旱事件的开始和结束的阈值设定为-1;
规则 2:若相邻两场干旱事件之间的时间间隔仅为 1 d,且当天 SPEI 值小于 0,则合并这两场相邻
的干旱事件,合并后的历时为两场干旱事件历时之和,干旱强度为两场干旱事件的干旱强度之和,否
则,认定为两场独立的干旱事件;
规则 3:在空间尺度上,若某日研究区范围内有≥5% 的格点干旱指数小于-1,且连续 15 个干旱日
之间格点重合率≥50%,则判定为一场时空连续的干旱事件。
4.1 验证干旱事件特征量的理论函数方程
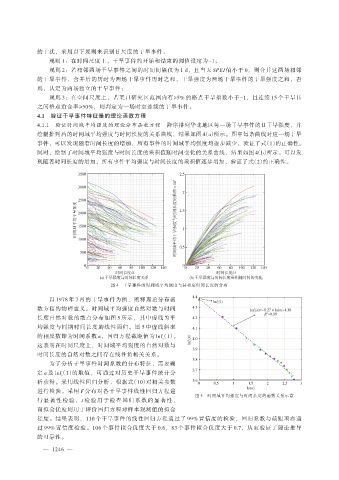
4.1.1 验证时间域平均强度的理论分布函数方程 降序排列华北地区每一场干旱事件的日干旱强度,并
绘制排列后的时间域平均强度与时间长度的关系曲线,结果如图 4(a)所示。图中每条曲线对应一场干旱
事件,可以发现随着时间长度的增加,所有事件的时间域平均强度均逐步减少,验证了式(1)的正确性。
同时,绘制了时间域平均强度与时间长度的乘积值随时间变化的关系曲线,结果如图 4(b)所示。可以发
现随着时间长度的增加,所有事件平均强度与时间长度的乘积值逐步增加,验证了式(2)的正确性。
图 4 干旱事件的时间域平均强度与其相应时间长度的分布
以 1978 年 7 月的干旱事件为例,阐释理论分布函
数方程的物理意义。时间域平均强度自然对数与时间
长度自然对数的散点分布如图 5 所示,其中虚线为平
均强度与同期时间长度的线性回归。图 5 中虚线斜率
的相反数即为时间系数 a,回归方程截距值为 lnI(1)。
e
这表明在时间尺度上,时间域平均强度的自然对数与
时间长度的自然对数之间存在线性负相关关系。
为了分析干旱事件时间系数的分布特征,需要确
定 a 及 lnI(1)的取值,可通过对历史干旱事件统计分
e
析获得。采用线性回归分析,根据式(10)对相关参数
进行检验。采用 F 分布对各干旱事件线性回归方程进
图 5 时间域平均强度与时间长度的函数关系示意
行显著性检验,t 检验用于检查回归系数的显著性,
而拟合优度则用于评价回归方程对样本观测值的拟合
程度。结果表明,110 个干旱事件的线性回归方程通过了 99% 置信度的检验,回归系数与截距项亦通
过 99% 置信度检验。106 个事件拟合优度大于 0.6,83 个事件拟合优度大于 0.7,从而验证了理论推导
的可靠性。
— 1246 —