Page 138 - 2025年第56卷第9期
P. 138
辨率为日,空间分辨率为 0.25°×0.25°。许多学者已将该数据集与多套观测资料进行了对比分析,发现
GLDAS-2.0 在中国东部地区的适用效果较好 [21-24] 。
3 干旱强度的理论分布函数方程推导
3.1 时间域上干旱强度的理论分布函数方程 以日尺度干旱事件为例进行理论分析,将时间维度上,
所有发生干旱格点的干旱指数与阈值差值的绝对值总和记作干旱强度。时间域上干旱强度的理论分布
函数推导分为以下三个步骤。
第一步,对日干旱强度序列进行降序排列,对此新序列识别时间域平均强度和时间长度的非线性
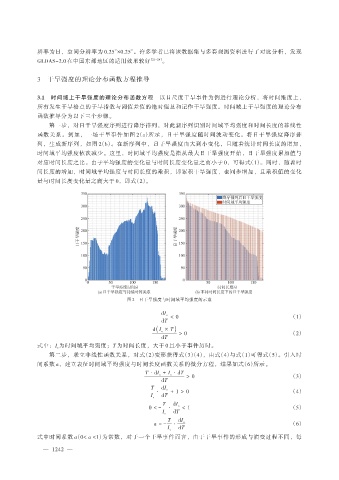
函数关系。例如,一场干旱事件如图 2(a)所示,日干旱强度随时间波动变化。将日干旱强度降序排
列,生成新序列,如图 2(b)。在新序列中,日干旱强度由大到小变化,且随着统计时间长度的增加,
时间域平均强度依次减少。这里,时间域平均强度是指从最大日干旱强度开始,日干旱强度累加值与
对应时间长度之比。由于平均强度的变化量与时间长度变化量之商小于 0,可得式(1)。同时,随着时
间长度的增加,时间域平均强度与时间长度的乘积,即累积干旱强度,也同步增加,且乘积值的变化
量与时间长度变化量之商大于 0,即式(2)。
图 2 日干旱强度与时间域平均强度的示意
dI e (1)
dT < 0
d( I e × T )
dT > 0 (2)
式中:I 为时间域平均强度;T 为时间长度,大于 0 且小于事件历时。
e
第二步,联立非线性函数关系,对式(2)变形获得式(3)(4),由式(4)与式(1)可得式(5)。引入时
间系数 a,建立表征时间域平均强度与时间长度函数关系的微分方程,结果如式(6)所示。
T ⋅ dI e + I e ⋅ dT
dT > 0 (3)
T dI e
⋅ + 1 > 0 (4)
I e dT
T dI e
0 < - ⋅ dT < 1 (5)
I e
T
a = - ⋅ dI e (6)
I e dT
式中时间系数 a(0< a <1)为常数,对于一个干旱事件而言,由于干旱事件的形成与演变过程不同,每
— 1242 —