Page 139 - 2025年第56卷第9期
P. 139
个干旱事件的时间系数也有所不同。
第三步,求解微分方程,可得时间域平均强度与时间长度的函数方程(11),理论推导如下。
变换式(6),得到式(7)
1 1
-a ⋅ dT = dI e (7)
T I e
变换式(7),得到式(8)
-a ⋅ d( lnT) = d( lnI e) (8)
对等式左右同时积分
n n
∫ - a ⋅ d( lnT) = ∫ ( ) (9)
d lnI e
1 1
式中 n 为重排序列的统计时间长度;
lnI e( n) = -alnn + lnI e(1) (10)
式中:I(n)为时间域平均强度;lnI(1)为常数,I(1)≥1,代表时间长度等于 1 时的理论时间域平均强度。
e
e
e
I e( n) = I e(1) ⋅ n -a (11)
式(11)为时间域平均干旱强度与时间长度之间的函数方程。如式(10)(11)所示,时间域平均强度的
自然对数与时间长度的自然对数呈线性负相关关系,时间域平均强度与时间长度的负指数幂之间成正比。
3.2 空间域上干旱强度的理论分布函数方程 将空间维度上格点的干旱强度累加值记作格点干旱强
度,干旱发生面积(格点数)的并集记为覆盖面积。空间域上干旱强度的理论分布函数推导分为以下三
个步骤。
第一步,对发生干旱的每个格点的干旱强度降序排列,对此新格点序列识别空间域平均强度与覆
盖面积的非线性函数关系。
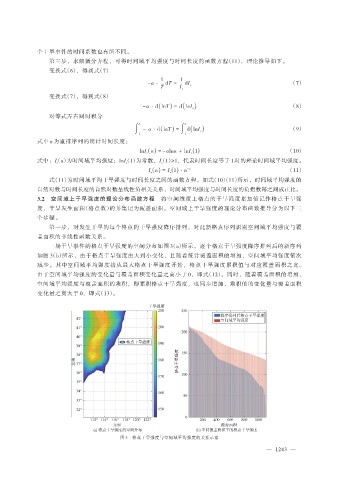
一场干旱事件的格点干旱强度的空间分布如图 3(a)所示。逐个格点干旱强度降序排列后的新序列
如图 3(b)所示,由于格点干旱强度由大到小变化,且随着统计覆盖面积的增加,空间域平均强度依次
减少。其中空间域平均强度指从最大格点干旱强度开始,格点干旱强度累积值与对应覆盖面积之比。
由于空间域平均强度的变化量与覆盖面积变化量之商小于 0,即式(12)。同时,随着覆盖面积的增加,
空间域平均强度与覆盖面积的乘积,即累积格点干旱强度,也同步增加,乘积值的变化量与覆盖面积
变化量之商大于 0,即式(13)。
图 3 格点干旱强度与空间域平均强度的关系示意
— 1243 —