Page 143 - 2025年第56卷第9期

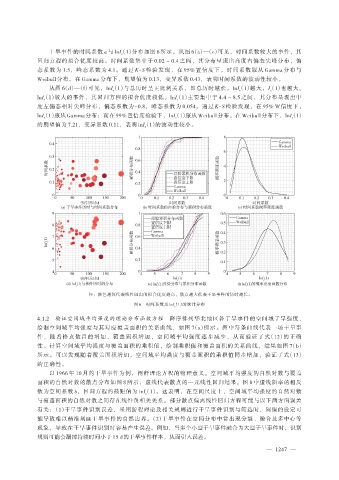
干旱事件的时间系数 a 与 lnI（1）分布如图 6 所示。从图 6（a）—（c）可见，时间系数较大的事件，其
e
回归方程的拟合优度较高。时间系数集中于 0.02 ~ 0.4 之间，其分布呈现出高度右偏态尖峰分布，偏
态系数为 1.5，峰态系数为 4.1。通过 K-S 检验发现，在 95% 置信度下，时间系数服从 Gamma 分布与
Weibull 分布。在 Gamma 分布下，期望值为 0.13，变异系数 0.43，表明时间系数的波动性较小。
从图 6（d）—（f）可见，lnI（1）与总历时呈正比例关系，即总历时越长，lnI（1）越大，I（1）也越大。
e
e
e
lnI（1）较大的事件，其回归方程的拟合优度较低。lnI（1）主要集中于 4.4 ~ 8.5 之间，其分布呈现出中
e
e
度左偏态相对尖峰分布，偏态系数为-0.8，峰态系数为 0.054。通过 K-S 检验发现，在 95% 置信度下，
lnI（1）服从 Gamma 分布；而在 99% 置信度检验下，lnI（1）服从 Weibull分布。在 Weibull分布下，lnI（1）
e
e
e
的期望值为 7.21，变异系数 0.11，表明 lnI（1）的波动性较小。
e

注：颜色越深代表线性回归的拟合优度越高，散点越大代表干旱事件的历时越长。
图 6 时间系数及 lnI（1）的统计分布
e
4.1.2 验证空间域平均强度的理论分布函数方程 降序排列华北地区各干旱事件的空间域干旱强度，
绘制空间域平均强度与其对应覆盖面积的关系曲线，如图 7（a）所示。图中每条曲线代表一场干旱事
件，随着格点数目的增加，覆盖面积增加，空间域平均强度逐步减少，从而验证了式（12）的正确
性。计算空间域平均强度与覆盖面积的乘积值，绘制乘积值和覆盖面积的关系曲线，结果如图 7（b）
所示。可以发现随着覆盖面积增加，空间域平均强度与覆盖面积的乘积值同步增加，验证了式（13）
的正确性。
以 1966 年 10 月的干旱事件为例，阐释理论方程的物理意义。空间域平均强度的自然对数与覆盖
面积的自然对数的散点分布如图 8 所示，虚线代表散点的一元线性回归结果。图 8 中虚线斜率的相反
数为空间系数 b，回归方程的截距值为 lnI（1）。这表明，在空间尺度上，空间域平均强度的自然对数
s
与覆盖面积的自然对数之间存在线性负相关关系。部分散点偏离线性回归方程可能与以下两方面误差
有关：（1）干旱事件识别误差，采用游程理论及相关规则进行干旱事件识别与筛选时，阈值的设定可
能导致难以精准刻画干旱事件的自然边界。（2）干旱事件在空间分布中常出现分裂、融合及多中心等
现象，导致在干旱事件识别时容易产生误差。例如，当多个小型干旱事件融合为大型干旱事件时，识别
规则可能会漏掉持续时间小于 15 d的干旱事件样本，从而引入误差。

— 1247 —