Page 82 - 2025年第56卷第9期

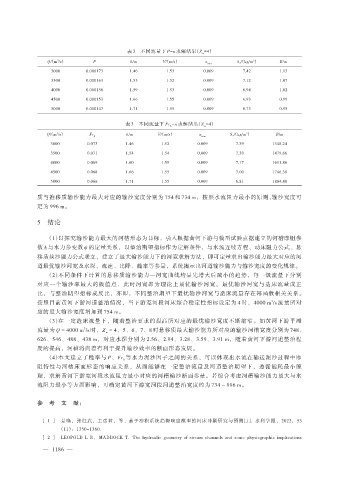
表 2 不同流量下 P-n 求解结果（Z =4）
w
Q/（m³/s） P h/m V/（m/s） n S /（kg/m³） B/m
min *
3000 0.000173 1.46 1.53 0.009 7.42 1.13
3500 0.000163 1.53 1.52 0.009 7.12 1.07

4000 0.000156 1.59 1.53 0.009 6.94 1.02
4500 0.000153 1.66 1.55 0.009 6.93 0.99
5000 0.000147 1.71 1.55 0.009 6.75 0.95

表 3 不同流量下 Fr -n 求解结果（Z =4）
A w
Q/（m³/s） Fr h/m V/（m/s） n S /（kg/m³） B/m
A min *
3000 0.073 1.46 1.52 0.009 7.39 1348.24
3500 0.071 1.54 1.54 0.009 7.30 1479.66
4000 0.069 1.60 1.55 0.009 7.17 1611.86

4500 0.068 1.66 1.55 0.009 7.00 1746.38
5000 0.066 1.71 1.55 0.009 6.81 1884.48

质与推移质输沙能力最大对应的输沙宽度分别为 754 和 734 m，按照水流阻力最小的原则，输沙宽度可
定为 996 m。

5 结论

（1）以探究输沙能力最大的河槽形态为目标，引入根据黄河下游与模型试验点据建立的河槽摩阻参
数 A 与水力参变数 ψ 的定量关系，以整治期望指标作为定解条件，与水流连续方程、动床阻力公式、悬
移质挟沙能力公式联立，建立了最大输沙能力下的河宽求解方法，即可定量求出输沙能力最大对应的河
道最优输沙河宽及水深、流速、比降、糙率等参量，系统揭示出河道输沙能力与输沙宽度的变化规律。
（2）不同条件下计算的悬移质输沙能力—河宽曲线均呈先增大后减小的趋势，每一级流量下分别
对应一个输沙率最大的极值点，此时河宽即为理论上最优输沙河宽。最优输沙河宽与造床流量成正
比，与整治期望指标成反比，亦即，不同整治期望下最优输沙河宽与造床流量存在幂函数相关关系。
按照目前黄河下游河道整治情况，当下游宽河段河床综合稳定性指标设定为 4 时，4000 m /s 流量所对
3
应的最大输沙宽度增加到 754 m。
（3）在一定造床流量下，随着整治要求的提高所对应的最优输沙宽度不断缩窄。如黄河下游平滩
流量为 Q = 4000 m /s 时，Z = 4、5、6、7、8 时悬移质最大输沙能力所对应的输沙河槽宽度分别为 748、
3
w
626、546、488、438 m，对应水深分别为 2.56、2.94、3.28、3.59、3.91 m，随着黄河下游河道整治程
度的提高，河槽将向着有利于提升输沙效率的断面形态发展。
（4）本文建立了糙率与 P、Fr 等水力泥沙因子之间的关系，可以体现出水流在输送泥沙过程中摩
A
阻特性与河槽床面形态的响应关系，从而能够在一定整治流量及河道整治期望下，遵循能耗最小原
理，求解黄河下游宽河段水流阻力最小对应的河槽输沙断面参量。若综合考虑河槽输沙能力最大与水
流阻力最小等方面影响，可确定黄河下游宽河段河道整治宽度约为 734 ~ 996 m。

参 考 文 献：

.
［ 1 ］ 景唤，张红武，王彦君，等 . 基于冲积系统趋衡响应模型的河床冲刷研究与预测［J］ 水利学报，2022，53
（11）：1350-1360.
［ 2 ］ LEOPOLD L B， MADDOCK T. The hydraulic geometry of stream channels and some physiographic implications
— 1186 —