Page 81 - 2025年第56卷第9期

图 5 推移质输沙能力最大条件下的最佳河宽求解结果
（2）通过上述已知的床沙及悬沙级配条件、最大输沙流量，给出不同的 P，假定一个流速 V ，可以
0
得到对应的比降 J；
（3）将求得的 J 与给出的河宽 B 代入连续方程，求出某一流量条件下的断面平均水深 h；
（4）根据上述参数计算出水力参变数 ψ，进而求出相应的摩阻参数 A 及河槽综合糙率 n，将求出的
n、h、J 值代入式（10）反求流速 V，若 V 与 V 不相等则改变初始假定流速反复试算；
0
（5）点绘出不同比降下的 P 与 n 的曲线变化图，此时可观察出曲线存在极小值。
用同样的思路也可以计算出 Fr -n 的关系曲线。下面给出黄河下游特定整治期望指标 Z 、输沙流量
A w
Q 下 ， 不 同 河 宽 、 比 降 下 的 曲 线 算 例（本 算 例 中 悬 沙 中 值 粒 径 d = 0.03 mm， 床 沙 中 值 粒 径 D =
50 50
0.08 mm），算例计算结果见图 6—7 和表 2—3。

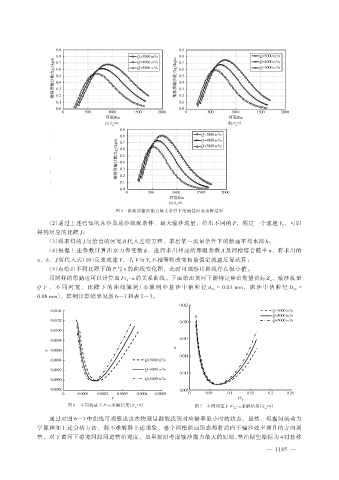
图 6 不同流量下 P-n 求解结果（Z =4） 图 7 不同河宽下 Fr -n 求解结果（Z =4）
w
A w
通过对图 6—7 中曲线可观察出这些物理量都能找到对应糙率最小时的状态，显然，根据河流动力
学原理和上述分析方法，都不难解释上述现象，整个河槽断面形态都将趋向于输沙效率提升的方向调
整。对于黄河下游宽河段河道整治宽度，如果按照考虑输沙能力最大的原则，整治期望指标为 4 时悬移

— 1185 —