Page 77 - 2025年第56卷第9期

动理论时，提出控制沙垄阻力大小的水力参变数 ψ 为 ［29］ ：

γ s - γ D 35
ψ = （7）
γ R′ b J
( R′ b J)
式中：D 35 为小于该粒径的重量占 35% 的床沙粒径，m；R b ′为表征沙粒阻力对应的水力半径，m。从而
定义 A = f γ s - γ D 35 。其中 R′ b 可由 Einstein 和 Barbarossa 对 Keulegan 对数流速分布公式合并而成的
γ
( k s )
下式试算求得：

u = 5.75 gR′ b J lg 12.27 χR′ b （8）
式中：χ 为校正系数，通过查表获得；k 为床面粗糙度。
s
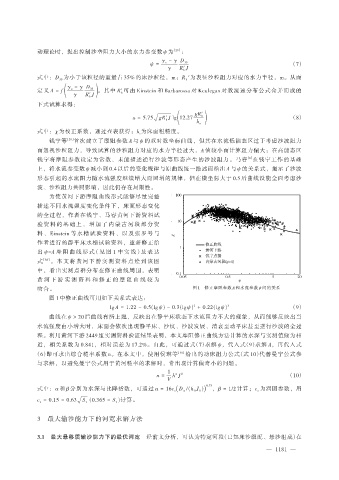
钱宁等 ［28］ 首次建立了摩阻参数 A 与 ψ 的双对数坐标曲线，但其在水流低能态区过于考虑沙波阻力
而忽视沙粒阻力，导致试算的沙粒阻力对应的水力半径过大，A 值较小而计算阻力偏大；在高能态区
［8］
钱宁将摩阻参数设定为常数，未能描述逆行沙波等形态产生的沙波阻力。马睿 在钱宁工作的基础
上，将水流参变数 ψ 减小到 0.4 以后的变化规律与原曲线统一描述而给出 A 与 ψ 的关系式，揭示了沙波
形态引起的水流阻力随水流强度继续增大而回增的规律，但在横坐标大于 0.5 后曲线没能全面考虑沙
波、沙粒阻力共同影响，因此仍存在局限性。
为使黄河下游摩阻曲线形式能够尽量完整
描述不同水流强度变化条件下，床面形态变化
的全过程，作者在钱宁、马睿黄河下游资料试
验 资 料 的 基 础 上 ， 增 加 了 内 蒙 古 河 段 部 分 资
料 、 Einstein 等 水 槽 试 验 资 料 、 以 及 张 罗 号 与
作者进行的静平床水槽试验资料，重新修正给
出 ψ-A 摩 阻 曲 线 形 式（见 图 1 中 实 线）及 表 达

式 ［30］ 。 本 文 将 黄 河 下 游 实 测 资 料 点 绘 到 该 图
中，看出实测点群分布在修正曲线周围，表明
黄 河 下 游 实 测 资 料 和 修 正 的 摩 阻 曲 线 较 为
吻合。 图 1 修正摩阻参数 A 和水流参数 ψ 间的关系
图 1 中修正曲线可用如下关系式表达：
2
lg A = 1.22 - 0.5(lg ψ) - 0.3(lg ψ) + 0.22(lg ψ) 3 （9）
曲线在 ψ > 20 后曲线有所上翘，反映出在静平床状态下水流阻力不大的现象，从而能够反映出当
水流强度由小增大时，床面会依次出现静平床、沙纹、沙波发展、消衰至动平床甚至逆行沙波的全过
程。利用黄河下游 2449 组实测资料验证结果表明，本文摩阻修正曲线方法计算的水深与实测值颇为相
近，相关系数为 0.841，相对误差为 17.2%。由此，可通过式（7）求解 ψ，代入式（9）求解 A，再代入式
（6）即可求出综合糙率系数 n。在本文中，使用侯琳等 ［30］ 给出的动床阻力公式（式 10）代替曼宁公式参
与求解，以避免曼宁公式用于黄河糙率的求解时，常出现计算值奇小的问题。
1 α β
n = h J （10）
V
式中：α 和 β 分别为水深与比降指数，可通过 α = 16c n( D m / (h 0 J 0 )) 0.75 ，β = 1/2 计算；c n 为涡团参数，用

c n = 0.15 - 0.63 S v (0.365 - S v )计算。

3 最大输沙能力下的河宽求解方法

3.1 最大悬移质输沙能力下的最优河宽 经前文分析，可认为特定河段（已知床沙级配、悬沙组成）在

— 1181 —