Page 79 - 2025年第56卷第9期

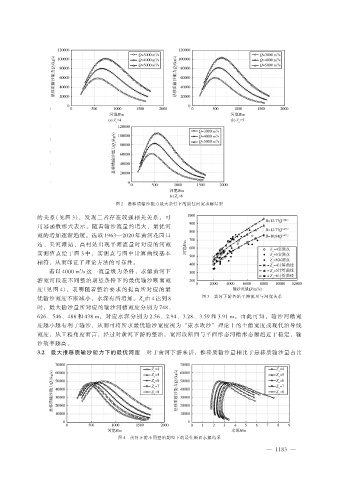
图 2 悬移质输沙能力最大条件下的最佳河宽求解结果

的关系（见图 3），发现二者存在较强相关关系，可
用幂函数形式表示。随着输沙流量的增大，最优河
宽的增加逐渐趋缓。选取 1963—2020 年黄河花园口
站、夹河滩站、高村站出现平滩流量时对应的河宽
实测值点绘于图 3 中，实测点与图中计算曲线基本
相符，从而印证了理论方法的可靠性。
若以 4000 m /s 这一流量级为条件，求解黄河下
3
游宽河段在不同整治期望条件下的最优输沙断面宽
度（见图 4），表明随着整治要求的提高所对应的最
图 3 黄河下游各站平滩流量与河宽关系
优输沙宽度不断减小，水深有所增加。Z 由 4 达到 8
w
时，最大输沙量所对应的输沙河槽宽度分别为 748、
626、546、488 和 438 m，对应水深分别为 2.56、2.94、3.28、3.59 和 3.91 m。由此可知，输沙河槽宽
度越小越有利于输沙，从而可将所求最优输沙宽度视为“束水攻沙”理论上的主槽宽度或现代治导线
宽度，从工程角度而言，经过对黄河下游的整治，宽河段断面与平面形态河槽形态越趋近于稳定，输
沙效率越高。
3.2 最大推移质输沙能力下的最优河宽 对于黄河下游来讲，推移质输沙量相比于悬移质输沙量占比

图 4 黄河下游不同整治期望下的最佳断面求解结果

— 1183 —