Page 24 - 2025年第56卷第10期

n 3
( x i - x ˉ)
n∑ i = 1
SK = （13）
(n - 1) (n - 2) δ 3
式中：n 为样本数量；x ˉ为样本 x n 均值； δ 为样本 x n 标准差。其中，SK = 0 为正态分布，SK > 0 为右偏
态分布，SK < 0 为左偏态分布。
日最低气温数据样本为邢台、石家庄和保定各站 1960—2025 年共 66 年 11 月到次年 2 月 7800 d 日
最低气温；采用式（13）可得到邢台、石家庄和保定站日最低气温矩法偏态系数 SK 分别为 0.10、0.22、
0.15； 日 最 低 气 温 七 日 累 计 值 T （7 Days’Accumulated Value of Daily Minimum Air Temperature，
7D
7DAVDMAT）是指当日及前 6 日连续 7 日的日最低气温和，例如 1 月 7 日累计气温，指的是 1 月 1—7 日日
最低气温的累计值。矩法偏态系数 SK 分别为 0.11、0.23、0.19，表明日最低气温和 T 均为偏态分布，
7D
且 0 < SK < 0.5，均为轻度右偏态。
3.3 累计分布概率和 TCI 分析 考虑冰情特征的气温寒潮指数法采用累计气温、降温幅度和降温的连
续性作为寒潮分类的指标参数。一般而言，气象站气温预报 7 天预见期具有较高参考价值，这里采用 T
7D
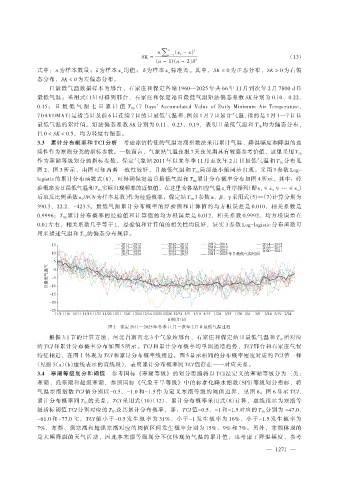
作为寒潮等级划分的指标参数。保定气象站 2011 年以来冬季 11 月至次年 2 月日最低气温和 T 分布见
7D
图 2、图 3 所示，由图可知两者一致性较好，日最低气温和 T 局部最小值同步出现。采用 3 参数 Log-
7D
logistic 的累计分布函数式（8），可得到保定站日最低气温和 T 累计分布概率分布如图 4 所示。其中：经
7D
验概率为日最低气温和 T 实际出现频率的近似值，在这里为各站相应气温 x i 升序排列（即 x 1 ≤ x 2 ≤ ⋯ ≤ x n ）
7D
后取反比例函数 n i /N （N 为样本总数）作为经验概率；保定站 T 3参数 α、β、γ采用式（5）—（7）计算分别为
7D
390.3、22.2、-423.5。最低气温累计分布概率的经验值和计算值的均方根误差是 0.010，相关系数是
0.9996；T 累计分布概率的经验值和计算值的均方根误差是 0.012，相关系数 0.9992。均方根误差在
7D
0.01 左右，相关系数几乎等于 1，经验值和计算值的相关性均良好，证实 3 参数 Log-logistic 分布函数可
用来描述气温和 T 的偏态分布规律。
7D

图 2 保定 2011—2025 年冬季 11 月—次年 2 月日最低气温过程
根据 3.1 节的计算方法，河北自南向北 3 个气象站邢台、石家庄和保定站日最低气温和 T 所对应
7D
的 TCI 和累计分布概率分布如图 5 所示。TCI 和累计分布概率均单调递增趋势，TCI 邢台和石家庄气候
特征相近，在图上体现为 TCI 和累计分布概率线接近。图 5 显示相同的分布概率密度对应的 TCI 值一样
（见图 5（a）（b）虚线表示的直线段），表明累计分布概率同 TCI 值存在一一对应关系。
3.4 寒潮等级划分和阈值 参考国标 《寒潮等级》 的划分思路将以 TCI 法定义的寒潮等级分为三类：
寒潮、强寒潮和超强寒潮，参照国标 《气象干旱等级》 中的标准化降水指数（SPI）等级划分指标，将
气温寒潮指数 TCI 值分别以-0.5、-1.0 和-1.5 作为定义寒潮等级的阈值边界，见图 6。图 6 显示 TCI、
累计分布概率同 T 的关系，TCI 采用式（10）（12）、累计分布概率采用式（8）计算，虚线指示为寒潮等
7D
级指标阈值 TCI 分别对应的 T 及其累计分布概率，即：TCI 值-0.5、-1 和-1.5 对应的 T 分别为 -47.0、
7D 7D
-61.0 和-77.0 ℃，TCI 值小于-0.5 发生概率为 31%、小于-1 发生概率为 16%、小于-1.5 发生概率为
7%，寒潮、强寒潮和超强寒潮对应的阈值区间发生概率分别为 15%、9% 和 7%。另外，寒潮体现的
是大幅降温的天气活动，因此本寒潮等级划分不仅体现负气温的累计值，也考虑了降温幅度，参考

— 1271 —