Page 38 - 水利学报2021年第52卷第2期

比降在 8‱～9‱左右，各流量级均有测得；二是近期最陡局部比降的小值增加，整个数据点分布的
重心上提。
文献［2］中通过数学模型的数值计算分析曾指出，随着出口水位的下降，芦家河水道沙泓中段的
最陡局部比降增幅趋于缩窄，主要表现为陡比降范围的扩展。这一认识有助于理解比降的实际变化
特点，即最陡局部比降变化幅度要明显小于较长范围的比降变化。实际上，短距离的比降变化对水
位变化的响应可以通过差分一维恒定流运动方程（式（1））并简化后进行识别。
æ Q 2 ö Q n 2
2
∂ ç ç ÷ ÷ + gA ∂z + g = 0 （1）
∂x è A ø ∂x AR 4/3
æ Q 2 Q 2 ö n 2 Q 2 n Q 2
2
J = 1 ç j + 1 - j ÷ + j + 1 j + 1 ϕ + j j (1 - ϕ ) （2）
2g∆x ç A 2 A 2 ÷ A 2 R 4/3 A R 4/3
2
è j + 1 j ø j + 1 j + 1 j j
式中：Q 为流量；A 为过水断面面积；z 为水位；n 为糙率；R 为水力半径；J 为离散断面之间比降；j
为离散断面标号； ∆x 为断面间距； ϕ 为权重因子。
令式（2）中右侧第一项为 J ，为速度水头比降；第 2、3 项合计为 J ，为能量损失比降。根据长江
f
v
中下游河道特性，短距离范围内流量一致，过水断面面积变化不大，J 可适当简化：
f
- 2 2
n Q
J = （3）
f
- 2-10/3
B H
以 200 m 范围内最陡局部比降作为分析对象，目前实测最大比降约 8‱～9‱，按 9‱计，则落差
约为 18 cm。为便于分析最陡局部比降区域末端水位下降对 J 的影响，需根据沙泓中段的实际情况进
行一系列合理概化：分析范围概化为矩形河槽，河宽统一按 500 m 计，平均水深按 3 m 计；流量按大
江流量 6000 m /s 时，沙泓分流比约 50%，取为 3000 m /s；参考下文中的图 6，流速沿程增加梯度取为
3
3
每百米增加 0.1 m/s。基于上述概化，9‱的水面比降中，速度水头比降、能量损失比降分别约为 2‱和 7‱。
假设下游水位下降引起最陡局部比降末端水位下降 10 cm，忽略式（3）左侧糙率与河宽变化，则 J f
增大约 0.8‱，在此基础上，引入一维连续性方程（式（4）），可试算进口水位，得 J 增大约 1.1‱，落
差仅增加约 2.2 cm。
V A = V j + 1 A j + 1 （4）
j
j
上述数值计算分析表明，当水位变幅与平均水深不在一个数量级时，即使是坡陡流急区，因流
速水头以及局部能量损失的变化幅度有限，距离较短，消纳下游水位降幅的能力也较为有限。具体
到芦家河水道沙泓中段而言，虽然近年来一直将 200 m 范围内的最陡局部比降作为衡量坡陡流急的重
要指标，但实际上并不能完全反映下游水位下降对坡陡流急现象的影响，其变化方向确实与整体比
降变化一致，可是幅度必然较弱。即最陡局部比降自三峡水库蓄水运用以来总体应是略有增加的，
但增幅有限，这与图 5 中近年来实测最陡局部比降最大值基本稳定于 8‱～9‱左右较为吻合。至于
图 5 中最陡局部比降的反复变化可能并非实际情况，而是与局部水尺的设置无法准确捕捉最陡区段，
以及江心定位、浪涌等因素造成的干扰有关，导致实测数据未能如实反映真实最陡比降。
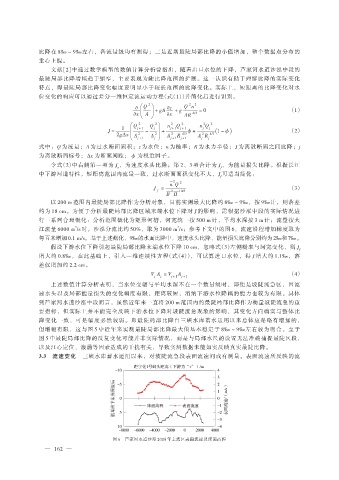
3.3 流速变化 三峡水库蓄水运用以来，对坡陡流急段表面流速间或有测量。表面流速所反映的流

图 6 芦家河水道沙泓 2018 年主流区表面流速及床面高程
— 162 —