Page 96 - 水利学报2021年第52卷第2期

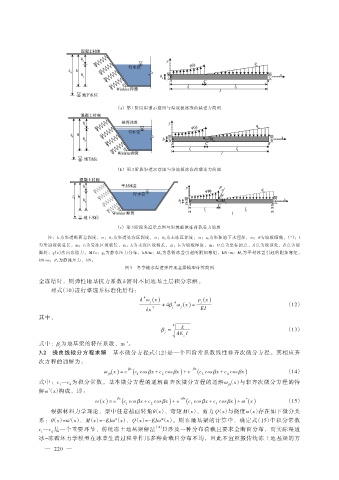
（a） 第 1 阶段渠道示意图与渠坡板冰冻荷载受力简图

（b） 第 2 阶段渠道示意图与渠坡板冰冻荷载受力简图

（c） 第 3 阶段渠道示意图与渠坡板冰冻荷载受力简图
注：h 为渠道断面总深度，m；h 1为渠道受冻区深度，m；h 2为未冻区深度，m；z 0为渠顶地下水埋深，m；θ为坡板倾角，（°）；l
为渠道坡板总长，m；l 1为受冻区坡板长，m；l 2为未冻区坡板长，m；b 1为坡板厚度，m；O 点为坐标原点，A 点为坡顶处，B 点为坡
脚处；q（x）法向冻胀力，MPa；q w为静水压力分布，kN/m；M ix为悬臂冰盖引起的附加弯矩，kN·m；M is为平封冰盖引起的附加弯矩，
kN·m；P is为静冰压力，kN。
图 3 冬季输水渠道弹性地基梁模型计算简图

全冻结时，则弹性地基抗力系数 k 需对不同地基土层积分求解。
对式（10）进行整理并标准化后得：
d ω ( ) x + 4β ω ( ) x = p ( ) x
4
j
j
4
dx 4 j j EI （12）
其中，
4 k
β = 4E I （13）
j
c
式中：β 为地基梁的特征系数，m 。
-1
j
3.2 挠曲线微分方程求解 基本微分方程式（12）是一个四阶常系数线性非齐次微分方程。其相应齐
次方程的通解为：
)
βx
-βx
ω ( ) x = e (c cos βx + c cos βx + e (c cos βx + c cos βx ) （14）
j0 1 2 3 4
式中：c —c 为积分常数。基本微分方程的通解由齐次微分方程的通解ω （x）与非齐次微分方程的特
1 4 j0
*
解ω（x）构成，即：
)
)
-βx
βx
*
ω ( ) x = e (c cos βx + c cos βx + e (c cos βx + c cos βx + ω ( ) x （15）
1 2 3 4
根据材料力学理论，梁中任意截面转角θ（x）、弯矩 M（x）、剪力 Q（x）与挠度ω（x）存在如下微分关
系：θ（x）=ω′ （x），M（x）=-EIω″ （x），Q（x）=-EIω‴ （x）。则在地基梁的计算中，确定式（15）中积分常数
c —c 是一个重要环节，传统冻土地基梁解法 ［18］ 只涉及一种分布荷载且要求全断面分布，而实际渠道
1 4
冰-冻破坏力学模型在冰盖生消过程中作用多种荷载且分布不均，因此不宜照搬传统冻土地基梁的方
— 220 —