Page 120 - 水利学报2021年第52卷第3期

述学者在图像识别方法上，均采用了基于阈值化的传统方法，该方法识别速度快但精度不足。随着
人工智能的发展，图像识别技术取得了新的进展。Jonathan 等 ［13］ 提出全卷积神经网络（Fully Convolu⁃
tional Networks，FCN），通过反卷积的方式使神经网络的数据分类能力从一维提升到二维，为深度学
习在图像识别方向上的应用提供了思路。何凯明等 ［14］ 通过残差学习设计了深度残差网络（Deep Resid⁃
ual Network，ResNet），极大提高了神经网络深度，并在此基础上提出 Mask-RCNN（Mask Region Con⁃
volutional Neural Network）图像识别模型 ［15］ ，为不同种类物体的识别与形状分析提供了基础。在级配
检测及相关领域，基于深度学习的图像识别方法尚未有成熟应用，但同样为级配检测提供了新的理
论依据与技术支持。
5 mm 以下的颗粒含量对于土石料级配合理性具有重要意义，我国规范对土石坝中 5mm 以下颗粒
含量作出了 20% ~ 50%之间的不同规定 ［16-18］ 。5 mm 以下的颗粒反映在土石料图像中呈现出细小、黏
连、形状不规则、堆叠现象严重的特征。对于此类图像，传统图像识别主要采用阈值化 ［19］ 、边缘检
测 ［20］ 和分水岭 ［21］ 等方法，深度学习图像识别主要采用全卷积神经网络 ［13］ 、视觉几何群网络 ［22］ 、深度
残差网络 ［14］ 、生成对抗网络 ［23］ 等语义分割方法。在采用不同方法试验后发现：针对土石料图像，传
统识别方法精度较差，尤其是对 5 mm 以下颗粒识别困难。深度学习方法的识别精度主要依靠模型设
计与标记的样本数量，土石料图像中存在大量的土石料颗粒，样本标记过程费时费力，且模型结构
复杂运行耗时，对计算机硬件要求高，方法限制较多。
针对传统图像识别方法精度差，深度学习方法效率低的缺陷，本文结合在传统图像识别方法中
广泛使用的基于最大类间方差阈值化的边缘检测算法 ［19］ 与基于深度学习的卷积神经网络模型，建立
了一种土石料图像快速识别与级配智能分析模型，深度阈值卷积模型（Deep Otsu Convolutional Neural
Network，DO-CNN）。经试验验证，模型能够显著提高级配检测的精度，且计算效率较高。

2 深度阈值卷积模型基本原理

2.1 边缘检测与最大类间方差法 深度阈值卷积模型基于最大类间方差法（Otsu 法）进行土石料图像
的颗粒边缘检测。图像中的边缘是指图像局部灰度剧烈变化的区域，在处理过程中，可将图像抽象
为二维函数 f（x，y），其中 x 与 y 代表各点在图像中所处位置，幅值 f 即为各对应点的像素值，也称
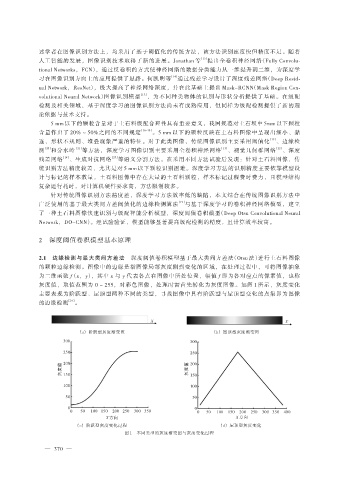
灰度值，取值范围为 0 ~ 255，对彩色图像，处理时需首先转化为灰度图像。如图 1 所示，灰度变化
主要表现为阶跃型、屋顶型两种不同的类型，寻找图像中具有阶跃型与屋顶型变化的点集即为图像
的边缘检测 ［24］ 。

（a） 阶跃型灰度渐变图 （b） 屋顶型灰度渐变图
300 300

250 250

灰度值 200 灰度值 200
150
150
100 100

50 50
0 0
0 50 100 150 200 250 300 350 0 50 100 150 200 250 300 350 400
X 方向 X 方向
（c） 阶跃型灰度变化过程 （d） 屋顶型灰度变化
图 1 不同类型的灰度渐变图与灰度变化过程

— 370 —