Page 90 - 2021年第52卷第8期

989
988
987
986
高程/m 985

984 1 月 4 日
1 月 19 日
983
2 月 22 日
982
2 月 28 日
981
400 450 500 550 600 650 700 750
距离/m
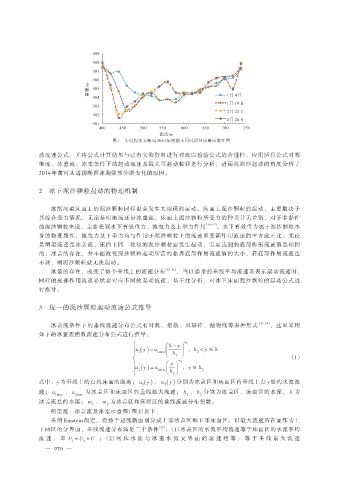
图 1 头道拐水文断面 2014 年冰期不同时段河床断面套汇图
动流速公式，并将公式计算结果与已有实测资料进行对比以检验公式的合理性，应用所得公式对明
渠流、冰盖流、冰塞条件下的起动流速及最大可起动粒径进行分析，进而从泥沙起动的角度分析了
2014 年黄河头道拐断面冰期强烈冲淤变化的原因。

2 冰下泥沙颗粒起动的物理机制

冰期河道床面上的泥沙颗粒同样也会发生大规模的运动。床面上泥沙颗粒的起动，主要取决于
其综合受力情况，无论是明渠流还是冰盖流，床面上泥沙颗粒所受力的种类并无差别，对于非黏性
的泥沙颗粒来说，主要受到水下有效重力、拖曳力及上举力作用 ［15-17］ 。水下有效重力属于泥沙颗粒本
身的物理属性，拖曳力及上举力均与作用于泥沙颗粒上的流速即底部作用流速的平方成正比。无论
是明渠流还是冰盖流，床面上同一粒径的泥沙颗粒要发生起动，需要达到的底部作用流速值是相同
的。冰盖的存在，并不能改变泥沙颗粒起动所需的临界底部作用流速值的大小，若底部作用流速达
不到，则泥沙颗粒就无法起动。
冰盖的存在，改变了整个垂线上的流速分布 ［18-21］ ，当以通常的垂线平均流速来表示起动流速时，
同样的底部作用流速必然会对应不同的起动流速，基于此分析，对冰下床面泥沙颗粒的起动公式进
行推导。

3 统一的泥沙颗粒起动流速公式推导

冰盖流条件下的垂线流速分布公式有对数、指数、双幂律、抛物线等多种形式 ［22-24］ ，这里采用
如下的冰盖流指数流速分布公式进行推导：
ì æ ℎ - y ö m 1
y
ï u ( ) = u 1max ç ÷ ，ℎ < y ≤ ℎ
ï 1 è ℎ 1 ø 2
í m （1）
ï æ y ö 2
u ( ) = u 2max ç ÷ ，y ≤ ℎ
y
ï 2 ℎ 2
î è 2 ø
y
y
式中：y 为垂线上的点到床面的距离； u ( ) 、 u ( ) 分别为冰盖区和床面区内垂线上点 y 处的水流流
1 2
速； u 、 u 为冰盖区和床面区的垂线最大流速； ℎ 、 ℎ 分别为冰盖区、床面区的水深， ℎ 为
1max 2max 1 2
冰盖流总的水深； m 、 m 为冰盖区和床面区的垂线流速分布指数。
1 2
明渠流、冰盖流及冰塞示意图（图 2）如下：
采用 Einstein 假定，将整个过流断面划分成上部冰盖区和下部床面区，以最大流速所在面作为上
下两区的分界面，垂线流速分布满足三个条件 ［25］ ：（1）冰盖区的水流平均流速等于床面区的水流平均
流 速 ， 即 U = U = U ；（2）河 床 水 流 与 冰 盖 水 流 交 界 面 的 流 速 相 等 ， 等 于 垂 线 最 大 流 速
1 2
— 970 —