Page 94 - 2021年第52卷第8期

40 0.25
0.20
35
0.15
（cm/s） 30 误差率 0.10
0.05
计算值/ 25 -0.05 1 2 3 4 5 6 7 8
0.00
20 -0.10 D1=0.32mm
-0.15 D2=0.85mm
15 -0.20 D3=1.32mm
15 20 25 30 35 40
试验值/（cm/s） B/h
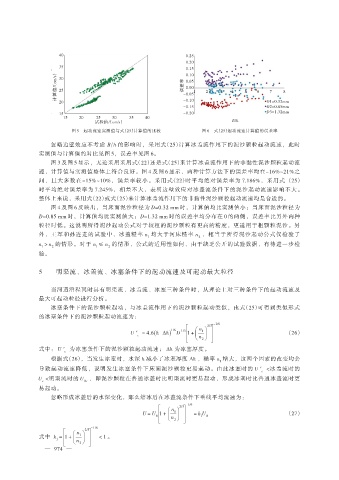
图 5 起动流速实测值与式（25）计算值的比较 图 6 式（25）起动流速计算值的误差率

忽略边壁效应不考虑 B ℎ 的影响时，采用式（25）计算冰盖流作用下的泥沙颗粒起动流速，此时
实测值与计算值的对比见图 5，误差率见图 6。
图 3 及图 5 显示，无论采用采用式（22）还是式（25）来计算冰盖流作用下的非黏性泥沙颗粒起动流
速，计算值与实测值整体上符合良好。图 4 及图 6 显示，两种计算方法下的误差率均在-16%~21%之
间，且大多数在-15%~10%，误差率较小。采用式（22）时平均绝对误差率为 7.186%，采用式 （25）
时平均绝对误差率为 7.245%，相差不大，表明边壁效应对冰盖流条件下的泥沙起动流速影响不大。
整体上来说，采用式（22）或式（25）来计算冰盖流作用下的非黏性泥沙颗粒起动流速均是合适的。
图 4 及图 6 反映出，当床面泥沙粒径为 D=0.32 mm 时，计算值均比实测值小；当床面泥沙粒径为
D=0.85 mm 时，计算值均比实测值大；D=1.32 mm 时的误差率均分布在 0 的两侧，误差率比另外两种
粒径时低。这说明所得泥沙起动公式对于较粗的泥沙颗粒有更高的精度，更适用于粗颗粒泥沙。另
外，王军和孙连进的试验中，冰盖糙率 n 均大于河床糙率 n ，相当于所得泥沙起动公式仅检验了
1 2
n > n 的情形。对于 n ≤ n 的情形，公式的适用性如何，由于缺乏公开的试验数据，有待进一步检
1 2 1 2
验。

5 明渠流、冰盖流、冰塞条件下的起动流速及可起动最大粒径

当河道沿程同时具有明渠流、冰盖流、冰塞三种条件时，从理论上对三种条件下的起动流速及
最大可起动粒径进行分析。
冰塞条件下的泥沙颗粒起动，与冰盖流作用下的泥沙颗粒起动类似，由式（25）可得到类似形式
的冰塞条件下的泥沙颗粒起动流速为：
é æ n ö 2/3 ù -1/6
U ′ = 4.6(ℎ−∆ℎ ) D 1/3 ê 1 + ç n 1 ÷ ú ú （26）
1/6
ê
c
ë è 2 ø û
式中： U ′ 为冰塞条件下的泥沙颗粒起动流速； ∆ℎ 为冰塞厚度。
c
根据式（26），当发生冰塞时，水深 ℎ 减小了冰塞厚度 ∆ℎ ，糙率 n 增大，这两个因素的改变均会
1
导致起动流速降低，说明发生冰塞条件下床面泥沙颗粒更易起动。由此冰塞时的 U ′ <冰盖流时的
c
U <明渠流时的 U 0c ，即泥沙颗粒在普通冰盖时比明渠流时更易起动，形成冰塞时比普通冰盖流时更
c
易起动。
忽略形成冰盖后的水深变化，那么结冰后在冰盖流条件下垂线平均流速为：

é æ n ö 2/3 ù -1/6
U = U ê 1 + ç n 1 ÷ ú ú = k U 0 （27）
0 ê
1
ë è 2 ø û
é æ n ö 2/3 ù -1/6
式中 k = ê 1 + ç 1 ÷ ú < 1 。
1 ê n ú
ë è 2 ø û
— 974 —