Page 88 - 2022年第53卷第1期

表 1 水资源经济利用主体与水环境保护主体之间的讨价还价过程

实际值 分配水量×10 /m 3
4
轮次 目标值
排污总量/万 t 经济效益/亿元 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ
#1-1 BT=580 10.63 580 31544 80409 10250 4157 3167 1931 47526
第一轮
#1-2 ET=0.4 0.4 216.99 4678 870 271 203 1349 1067 450
#2-1 BT=560 9.24 560 31544 80849 4326 4157 3167 1931 29353
第二轮
#2-2 ET=0.8 0.8 317.75 6234 10176 271 2300 1349 1067 4404
#3-1 BT=510 6.17 510 8868 71699 4326 4157 3167 1931 7347
第三轮
#3-2 ET=2.0 2.0 400.52 8868 10539 2328 3612 3167 1931 7347
#4-1 BT=480 4.51 480 8868 42852 4326 4157 3167 1931 7347
第四轮
#4-2 ET=2.8 2.8 439.89 8868 17687 2328 4157 3167 1931 7347
#5-1 BT=460 3.41 460 8868 23622 4326 4157 3167 1931 7347
第五轮
#5-2 ET=3.5 3.5 461.69 8868 25246 4326 4157 3167 1931 7347

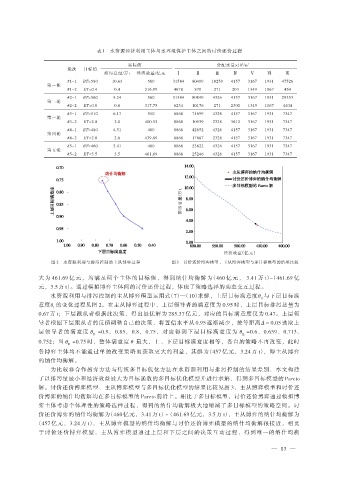
排污总量/万 t

经济效益（亿元）
图 2 水资源利用与排污控制的主从博弈过程 图 3 讨价还价博弈模型、主从博弈模型与多目标模型的结果比较

大为 461.69 亿元，均满足两个主体的目标值，得到纳什均衡解为（460 亿元， 3.41 万 t）~（461.69 亿
元，3.5 万 t）。通过模拟博弈主体间的讨价还价过程，体现了策略选择的动态交互过程。
水资源利用与排污控制的主从博弈模型运用式（7）—（10）求解，上层目标满意度θ 与下层目标满
U
意度θ 的变化过程见图 2。在主从博弈过程中，上层领导者的满意度为 0.95 时，上层目标排污总量为
L
0.67 万 t；下层跟从者根据此决策，得出最优解为 285.37 亿元，对应的目标满意度仅为 0.47。上层领
导者根据下层跟从者的反馈调整自己的决策，将置信水平从 0.95 逐渐减少，按等距离Δ = 0.05 选取上
层领导者的满意度 θ =0.9，0.85，0.8，0.75，对应得到下层目标满意度为 θ =0.6、0.659、0.713、
U L
0.752；当 θ =0.75 时，整体满意度 θ 最大，上、下层目标满意度相等，各自的策略不再改变，此时
U
各博弈主体均不能通过单独改变策略而获取更大的利益，其解为（457 亿元，3.24 万 t），即主从博弈
的纳什均衡解。
为比较非合作博弈方法与传统多目标优化方法在水资源利用与排污控制的结果差别，本文构建

了以排污量最小和经济效益最大为目标函数的多目标优化模型并进行求解，得到多目标模型的 Pareto
解。讨价还价博弈模型、主从博弈模型与多目标优化模型的结果比较见图 3，主从博弈模型和讨价还
价博弈的纳什均衡解均在多目标模型的 Pareto 前沿上。相比于多目标模型，讨价还价博弈通过模拟博
弈主体考虑个体理性的策略选择过程，得到的纳什均衡解极大地缩减了多目标模型的策略空间。讨
价还价博弈的纳什均衡解为（460 亿元，3.41 万 t）~（461.69 亿元，3.5 万 t），主从博弈的纳什均衡解为
（457 亿元，3.24 万 t），主从博弈模型的纳什均衡解与讨价还价博弈模型的纳什均衡解很接近，相比
于讨价还价博弈模型，主从博弈模型通过上层和下层之间的决策互动过程，得到唯一的纳什均衡

— 83 —