Page 46 - 2022年第53卷第2期

干旱事件 1 干旱事件 2
X 1

t p1 t p2
X 0
t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8

X 2

P I1
P I2
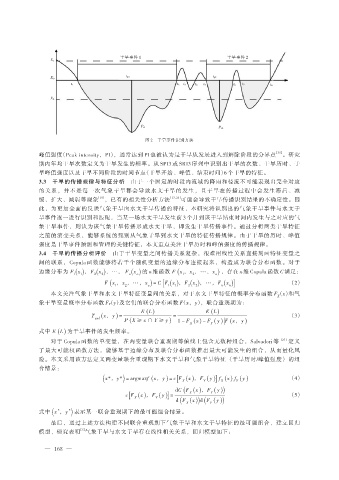
图 2 干旱事件识别方法

峰值强度（Peak intensity，PI），通常达到 PI 也被认为是干旱从发展进入到解除阶段的分界点 ［25］ 。研究
期内年均干旱次数定义为干旱发生的频率。从 SPI3 或 SRI3 序列中识别出干旱的次数、干旱历时、干
旱峰值强度以及干旱不同阶段的时间节点（干旱开始、峰值、结束时间）6 个干旱的特征。
3.3 干旱的传播规律与特征分析 由于一个固定的时段内流域的降雨和径流不可能表现出完全对应
的关系，并不是每一次气象干旱都会导致水文干旱的发生，且干旱在传播过程中会发生滞后、减
缓、扩大、减弱等现象 ［10］ ，已有的相关性分析方法 ［13，26］ 可能会导致干旱传播识别结果的不确定性。因
此，为更加全面的反映气象干旱向水文干旱传播的特征，本研究将识别出的气象干旱事件与水文干
旱事件逐一进行识别和匹配，当某一场水文干旱发生前 3 个月到该干旱结束时间内发生与之对应的气
象干旱事件，则认为该气象干旱传播形成水文干旱，即发生干旱传播事件。通过分析两类干旱特征
之前的演变关系，能够系统的甄别从气象干旱到水文干旱的特征传播规律。由于干旱的历时、峰值
强度是干旱事件预测和管理的关键特征，本文重点关注干旱历时和峰值强度的传播规律。
3.4 干旱的传播分析评价 由于干旱变量之间传播关系复杂，很难用线性关系直接刻画特征变量之
间的联系，Copula 函数能够将若干个随机变量的边缘分布连接起来，构造成为联合分布函数。对于
x
x
边缘分布为 F ( )，F ( )，…， F ( ) 的 n 维函数 F (x ，x ，⋯，x ) ，存在 n 维 Copula 函数 C 满足：
x
1 1 2 2 n n 1 2 n
x
x
x
F ( x ，x ，⋯，x ) = C [ F ( )，F ( )，⋯，F ( ) ] （2）
1 2 n 1 1 2 2 n n
本文关注气象干旱和水文干旱特征变量间的关系，对于水文干旱特征的概率分布函数 F（x）和气
X
象干旱变量概率分布函数 F Y （y）及它们的联合分布函数 F（x，y），联合重现期为：
E ( ) E ( )
L
L
)
T (x，y = = （3）
and P (X ≥ x ∩ Y ≥ y ) 1 - F ( ) x - F ( y | ) F (x，y )
Y
X
L
式中 E ( ) 为干旱事件的发生频率。
对于 Copula 函数的单变量，在两变量联合重现期等值线上包含无数种组合，Salvadori 等 ［27］ 定义
了最大可能权函数方法，能够基于边缘分布及联合分布函数推出最大可能发生的组合，从而量化风
险。本文采用该方法定义两变量联合重现期下水文干旱和气象干旱特征 （干旱历时/峰值强度） 的组
合情景：
)
]
( x*，y* = argmaxf (x，y = c[F ( ) x ，F ( ) f ( ) x f ( ) （4）
)
∗
y
y
X
Y
Y
X
dC (F ( ) x ，F ( ) )
y
]
Y
X
y
c[F ( ) x ，F ( ) = d (F ( ) x d (F ( ) ) （5）
)
X
Y
y
Y
X
式中 ( x ，y ∗ ) 表示某一联合重现期下的最可能组合情景。
∗
最后，通过上述方法构建不同联合重现期下气象干旱和水文干旱特征的最可能组合，建立回归
［5］
模型，研究表明 气象干旱与水文干旱存在线性相关关系，回归模型如下：
— 168 —