Page 64 - 2022年第53卷第3期

上三角上的图是 3 个权重系数的二维散点图，分析可知 W 和 W ，W 和 W 间的负相关性较高，相关系
1 2 1 3
数分别为-0.46 和-0.82，而 W 和 W 间的相关性较小，相关系数仅为-0.13。表 2 展示了各测点组合代
2 3
理模型的权重系数分布函数的最大后验概率估计值、均值和标准差，可以明显看出，对于每个测
点，SVR 的权重均值都比 Kriging 和 MARS 的大，说明 SVR 的预测性能最佳。同时，每个测点上 SVR
的权重标准差均比 Kriging 和 MARS 的稍大，说明 SVR 权重系数的不确定性也比 Kriging 和 MARS 的稍
大。取权重系数分布函数的最大后验概率估计值为权重系数的最终取值，通过加权求和，从而实现
组合代理模型的构建。
4.2 贝叶斯反演分析 将 4.1 节中建立的组合代理模型耦合到贝叶斯参数反演方法中，然后对 6 个覆
盖层的渗透系数进行反演分析。待反演渗透系数的先验分布设置为均匀分布，其取值范围如表 1 所
示。然后，采用 DREAM 算法评估待反演渗透系数的后验概率密度函数。其中，DREAM 算法的平
ZS ZS
行链设置为 4 条，迭代次数设为 10 000 次。前 6000 次迭代作为“燃烧期”，取后 4000 次迭代计算的样
本评估待反演渗透系数的后验概率密度函数。
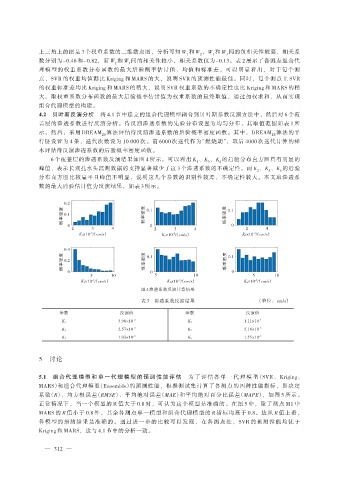
6 个覆盖层的渗透系数反演结果如图 4 所示。可以看出 K 、K 、K 的后验分布直方图具有明显的
1 3 4
峰值，表示长观孔水头监测数据的支持显著减少了这 3 个渗透系数的不确定性。而 K 、K 、K 的后验
2 5 6
分布直方图比较扁平且峰值不明显，说明这几个参数的识别性较差，不确定性较大。本文取渗透系
数的最大后验估计值为反演结果，如表 3 所示。

0.2
概率密度 0.1 概率密度 0.1 概率密度 0.1

0 0 0
2 3 4 2 3 4 2 4
K 1×10 /（cm/s） K 2×10 /（cm/s） K 3×10 /（cm/s）
-3
-2
-2
0.4
概率密度 0.2 概率密度 0.1 概率密度 0.1

0 0 0
5 10 5 10 5 10
K 4×10 /（cm/s） K 5×10 /（cm/s） K 6×10 /（cm/s）
-2
-3
-4
图 4 渗透系数反演计算结果
表 3 渗透系数反演结果 （单位：cm/s）
参数 反演值 参数 反演值
3.98×10 -2 1.11×10 -4
K 1 K 4
2.57×10 -2 5.18×10 -3
K 2 K 5
-3 -2
K 3 1.03×10 K 6 1.55×10

5 讨论

5.1 组 合 代 理 模 型 和 单 一 代 理 模 型 的 预 测 性 能 评 估 为 了 评 估 各 单 一 代 理 模 型（SVR、 Kriging、
MARS）和组合代理模型（Ensemble）的预测性能，根据测试集计算了各测点的四种性能指标，即决定
系数（R）、均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE），如图 5 所示。
正常情况下，当一个模型的 R 值大于 0.8 时，可认为这个模型是准确的。在图 5 中，除了测点 M1 中
MARS 的 R 值小于 0.8 外，其余各测点单一模型和组合代理模型的 R 指标均高于 0.8。故从 R 值上看，
各模型的预测结果是准确的。通过进一步的比较可以发现，在各测点处，SVR 的预测性能均优于
Kriging 和 MARS，这与 4.1 节中的分析一致。

— 312 —