Page 63 - 2022年第53卷第3期

（分别为 1327.17、1340.17、1316.10、1341.10、1329.20、1340.60、1335.08、1334.86 m），基于所提
出的贝叶斯框架下大坝渗流参数反演组合代理模型对 L 水电站坝基河床覆盖层的渗透系数开展反演
研究。
4.1 组合代理模型构建 根据现场勘探数据和室内试验数据，获得覆盖层岩体的渗透系数的取值范
围，如表 1 所示。假设 6 个覆盖层的渗透系数服从均匀分布，采用 LHS 方法抽取 100 个样本点，将
100 个样本点依次输入到耦合 VOF 法的三维非稳态水气两相流渗流模型 ［25］ 中进行模拟计算，得到 100
组长观孔水头模拟值，从而生成构建组合代理模型的数据集。随机选取 80 组样本作为训练集训练
SVR、Kriging 和 MARS 这三种代理模型，剩下的 20 组样本作为测试集测试代理模型的预测性能。采
用 DREAM 算法计算组合代理模型的权重系数，设置 3 条平行链，迭代次数设为 15 000 次，对迭代
ZS
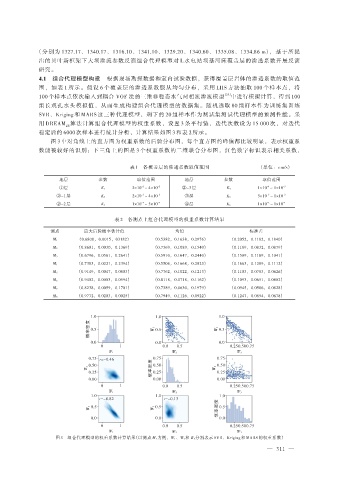
稳定后的 6000 次样本进行统计分析，计算结果如图 3 和表 2 所示。
图 3 中对角线上的直方图为权重系数的后验分布图，每个直方图的峰值都比较明显，表示权重系
数能被较好的识别；下三角上的图是 3 个权重系数的二维联合分布图，红色数字标识表示相关系数，

表 1 各覆盖层的渗透系数取值范围 （单位：cm/s）

地层 参数 取值范围 地层 参数 取值范围
①层 K 1 2×10 ～4×10 -2 ②-3 层 K 4 1×10 ～1×10 -3
-4
-2
②-1 层 K 2 2×10 ～4×10 -2 ③层 K 5 5×10 ～1×10 -2
-2
-3
②-2 层 K 3 1×10 ～5×10 -3 ④层 K 6 1×10 ～1×10 -1
-2
-3
表 2 各测点上组合代理模型的权重系数计算结果
测点 最大后验概率估计值 均值 标准差
（0.6800，0.0015，03182） （0.5382，0.1638，0.2976） （0.2052，0.1182，0.1840）
M 1
（0.8601，0.0030，0.1369） （0.7369，0.1089，0.1540） （0.1189，0.0832，0.0879）
M 2
（0.6796，0.0561，0.2641） （0.5910，0.1647，0.2440） （0.1509，0.1189，0.1041）
M 3
（0.7383，0.0221，0.2394） （0.5506，0.1668，0.2823） （0.1663，0.1289，0.1112）
M 1
（0.9149，0.0047，0.0803） （0.7762，0.1022，0.1213） （0.1103，0.0783，0.0626）
M 5
（0.9402，0.0003，0.0594） （0.8118，0.0718，0.1162） （0.1093，0.0651，0.0802）
M 6
（0.8238，0.0059，0.1701） （0.7389，0.0630，0.1979） （0.0945，0.0586，0.0828）
M 7
（0.9772，0.0203，0.0025） （0.7949，0.1126，0.0922） （0.1247，0.0894，0.0678）
M 8
1.0 1.0 1.0
概率密度 0.5 W 1 0.5 W 1 0.5

0.0 0.0 0.0
0 1 0.0 0.5 0.250.50 0.75
W 1 W 2 W 3
0.75 r=-0.46 0.75 0.75
0.50 0.50 0.50
W 2 概率密度 W 2
0.25 0.25 0.25
0.00 0.00 0.00
0 1 0.0 0.5 0.250.50 0.75
W 1 W 2 W 3
1.0 1.0 1.0
r=-0.82 r=-0.13
W 3 0.5 W 3 0.5 概率密度 0.5
0.0 0.0 0.0
0 1 0.0 0.5 0.250.50 0.75
W 1 W 2 W 3
图 3 组合代理模型的权重系数计算结果（以测点 M 1为例，W 1、W 2和 W 3分别表示 SVR、Kriging 和 MARS 的权重系数）
— 311 —