Page 60 - 2022年第53卷第3期

p ( ) p( | y θ )
θ
)
p( |y =
θ
)
p ( ) p( | y θ dθ
θ

y
x

R R

绝对偏差/m
MAPE/‰ MASE/m MAPE/‰ MASE/m
2.0

MAE/m MAE/m
W 1

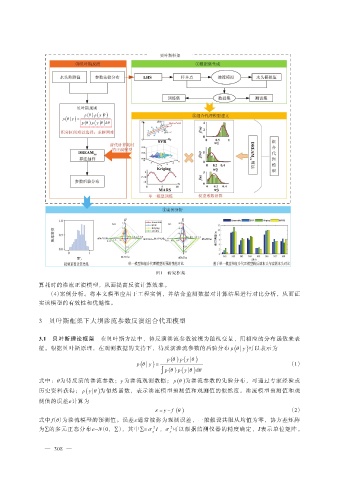
图 1 研究框架
算耗时的渗流正演模型，从而提高反演计算效率。
（4）案例分析。将本文模型应用于工程实例，并结合监测数据对计算结果进行对比分析，从而证
实该模型的有效性和优越性。

3 贝叶斯框架下大坝渗流参数反演组合代理模型

3.1 贝叶斯理论框架 在贝叶斯方法中，待反演渗流参数被视为随机变量，用相应的分布函数来表
)
征。根据贝叶斯原理，在观测数据的支持下，待反演渗流参数的后验分布 p(θ | y 可以表示为
θ
)
p(θ | y = p ( ) p( y |θ ) （1）
)
θ
 p ( ) p( y |θ dθ
θ
式中：θ为待反演的渗流参数；y 为渗流观测数据； p ( )为渗流参数的先验分布，可通过专家经验或
历史资料获得； p( y |θ )为似然函数，表示渗流模型预测值和观测值的似然度。渗流模型预测值和观
测值的误差ε计算为
ε = y - f ( ) （2）
θ
式中 f（θ）为渗流模型的预测值。误差ε通常被称为观测误差，一般假设其服从均值为零，协方差矩阵
为∑的多元正态分布ε~N（0，∑ ），其中∑= σ I ，σ 可以根据监测仪器的精度确定，Ι表示单位矩阵。
2
2
ε
ε
— 308 —