Page 124 - 2022年第53卷第4期
P. 124
Q Q Q Q
V = = = = (8)
Bh ζ h 3 ( k 2 h α 2 ) h 3 9 + 6α 2
2
2
2 æ ç n Q 2 - α 1 ö ÷ 22 + 12α 2
k 2 ç 4 ÷
è k 1 k 2 ø
式(5)—式(8)给出了主要水力因子与流量或水深之间的关系,均成单因素关系,即只需要已知
流量或水深,就可以求解其他所有主要水力因子,大大方便了应用,提高了解决实际问题的能力和
效率。
3 疏浚对降低洪水位效果计算方法
疏浚对河道的防洪作用可以通过两个参数分别评价,一个是同流量水位的下降值ΔH,另外一个
是平滩水位时行洪能力的增加值ΔQ,如何计算这两个变量,是本节需要解决的问题。
假定对某河道进行疏浚以降低洪水位,断面的疏浚面积为ΔA,疏浚深度为ΔZ,河道疏浚长度为
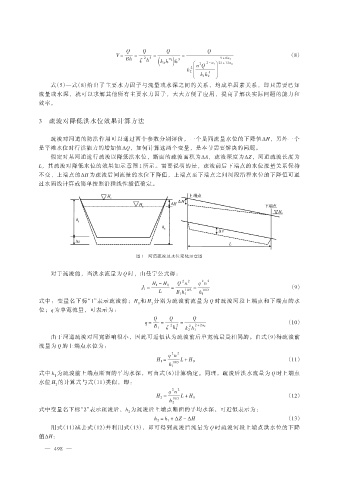
L,其疏浚对降低水位的效果如示意图 1 所示。需要说明的是,疏浚前后下端点的水位流量关系保持
不变,上端点的ΔH 为疏浚后同流量的水位下降值,上端点至下端点之间河段沿程水位的下降值可通
过水面线计算或简单按照沿程线性插值确定。
图 1 河道疏浚及水位变化示意图
对于疏浚前,当洪水流量为 Q 时,由曼宁公式得:
Q n 2 q n 2
2
2
J 1 = H 1 - H 0 = = (9)
L 10/3 10/3
B 1 h 1 h 1
式中:变量名下标“1”表示疏浚前;H 和 H 分别为疏浚前流量为 Q 时疏浚河段上端点和下端点的水
0 1
位;q 为单宽流量,可表示为:
Q Q Q
q = = = (10)
2 2 2 2 + 2α 2
B 1
ζ h 1
k 2 h 1
由于河道疏浚对河宽影响很小,因此可近似认为疏浚前后单宽流量是相同的。由式(9)得疏浚前
流量为 Q 的上端点水位为:
q n 2
2
H 1 = L + H 0 (11)
10/3
h 1
式中 h 为疏浚前上端点断面的平均水深,可由式(6)计算确定。同理,疏浚后洪水流量为 Q 时上端点
1
水位 H 的计算式与式(11)类似,即:
2
q n 2
2
H 2 = (12)
10/3 L + H 0
h 2
式中变量名下标“2”表示疏浚后,h 为疏浚后上端点断面的平均水深,可近似表示为:
2
h 2 = h 1 + ΔZ - ΔH (13)
用式(11)减去式(12)并利用式(13),即可得到疏浚后流量为 Q 时疏浚河段上端点洪水位的下降
值ΔH:
— 498 —