Page 53 - 2022年第53卷第4期

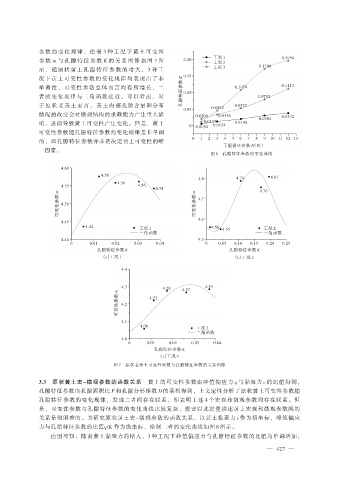
参 数 的 变 化 规 律 ， 绘 制 3 种 工 况 下 黄 土 可 变 性
参 数 m 与 孔 隙 特 征 参 数 K 的 关 系 图 像 如 图 7 所 0.20 工况 1 0.1956
工况 2
示，随原状 黄 土 孔 隙 特 征 参 数 的 增 大 ， 3 种 工 工况 3 0.1708
况下黄土可变性参数的变化规律均表现出了非
单调性，可变性参数总体而言均有所增长，二 孔隙特征参数 K 0.15 0.1074 0.1113
者的变化规律与三角函数接近。可以看出，对 0.10 0.0792
于 原 状 老 黄 土 而 言 ， 黄 土 内 部孔隙含量和分布 0.0522
0.05 0.0452
情况的改变会对微观结构的承载能力产生重大影 0.0204 0.0336
0.0304 0.0372
响，进而导致黄土可变性产生变化。但是，黄土 0.0117 0.0198
0 0.0054 0.0124
可变性参数随孔隙特征参数的变化规律是非单调
的，即孔隙特征参数并非是决定黄土可变性的唯 0 1 2 3 4 5 6 7 8 9 10 11 12 13
干湿循环次数 N（次）
一因素。
图 6 孔隙特征参数的变化曲线

4.60
4.58 4.81
4.8 4.79
4.56
4.55 4.56
4.54 4.76
可变性参数 m 4.50 可变性参数 m 4.7

4.6
4.45
4.44 4.56
工况 1 4.55 工况 2
三角函数 三角函数
4.40 4.5
0 0.01 0.02 0.03 0.04 0 0.05 0.10 0.15 0.20 0.25
孔隙特征参数 K 孔隙特征参数 K
（a）工况 1 （b）工况 2

4.4

4.3 4.28 4.27 4.29
可变性参数 m 4.2 4.22

4.1
4.06
工况 3
三角函数
4.0
0 0.01 0.02 0.03 0.04
孔隙特征参数 K
（c）工况 3
图 7 原状老黄土可变性参数与孔隙特征参数的关系图像

3.3 原状黄土宏-微观参数的函数关系 黄土的可变性参数由峰值偏应力 q 与黏聚力 c 的比值得到，
孔隙特征参数由孔隙面积比 F 和孔隙分形维数 D 的乘积得到，上文定性分析了原状黄土可变性参数随
孔隙特征参数的变化规律，发现二者间存在联系，即表明上述 4 个宏观和微观参数间存在联系。但
是，可变性参数与孔隙特征参数的变化曲线比较复杂，想要以此定量描述黄土宏观和微观参数间的
关系是很困难的。为研究原状黄土宏-微观参数的函数关系，以黄土黏聚力 c 作为横坐标，峰值偏应
力与孔隙特征参数的比值q/K 作为纵坐标，绘制二者的变化曲线如图 8 所示。
由图可知，随着黄土黏聚力的增大，3 种工况下峰值偏应力与孔隙特征参数的比值均单调增加，

— 427 —