Page 55 - 2022年第53卷第8期
P. 55
2.4 渗流- 溶蚀耦合分析方程 孔隙溶液中溶质迁移的对流速率在无流动
水中为零,当环境水存在水力梯度时,根据渗流微分方程计算对流速率。
根据达西定律建立的渗流微分方程为:
( θρ )
+ ·( ρ u) =Q
Δ
t m
( 12)
k
u =- ( p + ρ g)
Δ
ρ g
3
3
式中:ρ 为水的密度,kg?m ;Q 为源汇项,kg?(m·s);p为孔隙水压力,
m
2
Pa;g为重力加速度,m?s;k为渗透系数,m?s。水泥基材料的渗透系数
通常为孔隙率的函数,根据 Kozeny - Carman(K - C)方程可得渗透系数的演
化方程为 [25] :
2
1 - θ 0
) 3 ( ) (13)
0
k = k( θ ? θ 0 1 - θ
为初始孔隙率,本文取混凝土水化完全
0
式中:k 为初始渗透系数,m?s;θ 0
时( h = 1 )的孔隙率作为初始孔隙率。
α
图 2为渗流- 溶蚀耦合求解过程流程图,通过式(12)计算出孔隙溶液
对流速率,进而影响式( 2)中钙离子在多孔介质中的传输通量,改变钙离
子扩散系数,进而实现钙离子的迁移扩散,混凝土孔隙率增加,渗透系数
图 2 渗流- 溶蚀耦合求解
变大,从而对渗流场产生影响,实现渗透溶蚀耦合过程。基于钙离子在水
过程流程图
泥基体孔隙溶液中的质量守恒定律公式(1)和渗流微分方程式(12),建立
混凝土防渗墙渗透溶蚀耦合非线性偏微分方程组,采用有限元法进行数值求解,运用 COMSOLMul
tiphysics 软件中的达西定律模块及溶质运移模块进行渗流场和溶质运移场的耦合分析。
3 试验论证
本文采用文献[19]混凝土试件溶蚀算例进行模型验证,试件横断面尺寸为 100mm× 100mm,模
拟其全部浸泡在软水中的溶蚀情况,研究其溶蚀深度演化规律,混凝土配合比见表 1,有限元网格模
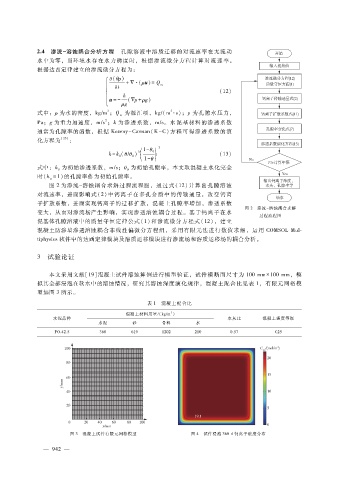
型如图 3所示。
表 1 混凝土配合比
3
混凝土材料用量?(kg?m )
水泥品种 水灰比 混凝土强度等级
水泥 砂 骨料 水
PO.42.5 368 619 1202 210 0.57 C25
图 3 混凝土试件有限元网格模型 图 4 试件浸泡 360d钙离子浓度分布
— 9 4 —
2