Page 88 - 2022年第53卷第10期
P. 88
量下水流强度更大,利津站同粒径下泥沙进入悬移运动的百分比就大一些,故计算公式中扬动概率系
数 a的取值大于花园口站的。进一步分析其他水文站资料也发现类似规律,从而某站的扬动概率系数
ss
a与泥沙粒径 d和某站与花园口站的比降之比有关,可近似用下式表示:
ss
HYK
- 0.6 J 1.6
a ss某站 = 0.18d ( ) (13)
J
某站
- 4
- 4
式中:J 为花园口站的比降,2.2 × 10 ;J 为某水文站的比降,利津站比降为 1 × 10 ,高村站比降
HYK 某站
- 4
为 1.4 × 10 。
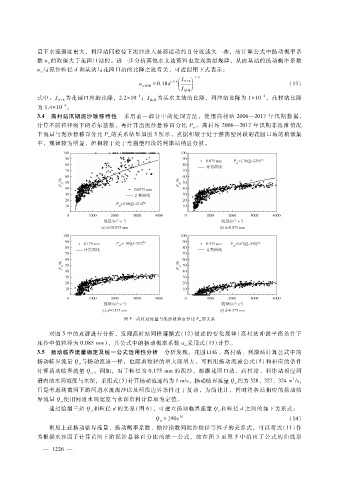
3.4 高村站汛期泥沙输移特性 采用前一部分中的处理方法,使用高村站 2006—2017年汛期数据,
计算不同粒径级下的希尔兹数,再计算出泥沙悬移百分比 P 。高村站 2006—2017年汛期非漫滩情况
ss
下流量与泥沙悬移百分比 P 的关系结果如图 5所示,点据相较于处于游荡型河段的花园口站的稍微集
ss
中,规律较为明显,但相较于处于弯曲型河段的利津站稍显分散。
图 5 高村站流量与泥沙悬移百分比 P ss 的关系
对图 5中的点群进行分析,发现高村站同样遵循式(12)描述的变化规律(高村站冲淤平衡条件下
床沙中值粒径为 0.085mm),其公式中的扬动概率系数 a采用式(13)计算。
ss
3.5 扬动临界流量确定及统一公式适用性分析 分析发现,花园口站、高村站、利津站计算公式中的
扬动临界流量 Q 与扬动流速一样,也随着粒径的增大而增大,可利用扬动流速公式(5)和相应的条件
ss
计算扬动临界流量 Q 。例如,对于粒径为 0.175mm的泥沙,根据花园口站、高村站、利津站相应河
ss
3
槽内的水面宽度与水深,采用式(5)计算扬动流速约为 1m?s,扬动临界流量 Q 约为 328、327、324m ?s,
ss
只是考虑到黄河下游河道水流泥沙以及河段边界条件过于复杂,为简化计,暂时将各站相应的扬动临
界流量 Q 使用河道水面宽度与水深资料计算取为定值。
ss
通过绘制三站 Q 和粒径 d的关系(图 6),可建立扬动临界流量 Q 和粒径 d之间的如下关系式:
ss ss
3d
Q = 190e (14)
ss
利用上述扬动临界流量、扬动概率系数、输沙指数同泥沙粒径等因子的关系式,可以将式( 11)作
为根据水沙因子计算黄河下游泥沙悬移百分比的统一公式,故在图 3至图 5中给出了公式的曲线形
— 1 2 6 —
2