Page 86 - 2022年第53卷第10期

［１ － ４．２ Ｓ（０．３６５ － Ｓ）］ （１０ｂ）
κ ＝ κ ０ 槡 Ｖ Ｖ
＝ ０．４ ，为清水卡门常数；Ｓ为体积含沙量。
式中：κ ０ Ｖ
按照近些年黄河汛期洪水流量减小一些的花园口水沙
３
资料（资料范围流量 Ｑ ＝ ２５８～１６００ｍ ?ｓ；平均流速 Ｖ ＝ ０．４８～
１．５５ｍ?ｓ；水面宽 Ｂ ＝ ３０５～８７８ｍ ；ｈ ＝ １．１２～１．１９ｍ ），使用
式（ １０ａ）计算发现黄河下游粒径小于或等于 ０．０２５ｍｍ的泥
沙，基本都 是 冲 泻 质，这 部 分 泥 沙 在 汛 期 基 本 被 形 容 为
“一泻千里，穿堂而过” ［３２ － ３３］ 。因此，使用修正后的 惠遇
甲和胡 春 宏 方 法 首 先 点 绘 了 花 园 口 站 流 量 与 粒 径 ｄ为
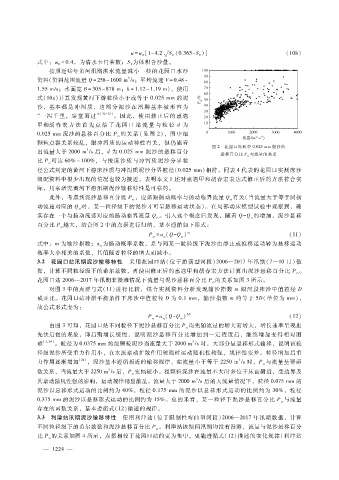
０．０２５ｍｍ泥沙的悬移百分比 Ｐ 的关系（见图 ２），图中细
ｓｓ
颗粒点群关系较乱，跟冲泻质的运动特性有关，但仍能看
图 ２ 花园口站粒径 ０．０２５ｍｍ泥沙的
３
出流量大于 ２０００ｍ ?ｓ后，ｄ为 ０．０２５ｍｍ泥沙的悬移百分
悬移百分比 Ｐ ｓｓ 与流量的关系
比 Ｐ 可达 ６０％～１００％，与按床沙质与冲泻质泥沙分界粒
ｓｓ
径公式判定的黄河下游床沙质与冲泻质泥沙分界粒径（ ０．０２５ｍｍ）相符，同表 ４代表的花园口实测床沙
级配资料中很少出现的情况也较为接近，表明本文上述对惠遇甲和胡春宏表达式修正后的方法符合实
际，用来研究黄河下游汛期泥沙输移特性是可靠的。
此外，考虑到泥沙悬移百分比 Ｐ ，应该跟扬动概率与扬动临界流量 Ｑ 有关（当流量大于等于同扬
ｓｓ
ｓｓ
动流速对应的 Ｑ 时，某一粒径级下的泥沙才可呈悬移运动状态）。在局部动床模型试验中观察到，确
ｓｓ
实存在一个与扬动流速对应的扬动临界流量 Ｑ 。引入这个概念后发现，随着 Ｑ － Ｑ 的增加，泥沙悬移
ｓｓ
ｓｓ
百分比 Ｐ 越大，结合图 ２中的点据进行归纳，基本遵循如下形式：
ｓｓ
Ｐ ＝ ａ（Ｑ － Ｑ ） ｍ （１１）
ｓｓ ｓｓ ｓｓ
式中：ｍ为输沙指数；ａ为扬动概率系数，系与同某一粒径级下泥沙由静止或推移运动转为悬移运动
ｓｓ
概率大小相关的系数，其值随着粒径的增大而减小。
３．２ 花园口站汛期泥沙输移特性 采用花园口站（位于游荡型河段）２００６—２０１７年汛期（７—１０月）数
据，计算不同粒径级下的希尔兹数，再使用修正后的惠遇甲和胡春宏方法计算出泥沙悬移百分比 Ｐ 。
ｓｓ
花园口站 ２００６—２０１７年汛期非漫滩情况下流量与泥沙悬移百分比 Ｐ 的关系如图 ３所示。
ｓｓ
对图 ３中的点群与式（１１）进行比较，结合实测资料分析发现输沙指数 ｍ跟河段床沙中值粒径 Ｄ
成正比。花园口站冲淤平衡条件下床沙中值粒径 Ｄ为 ０．１ｍｍ，输沙指数 ｍ约等于 ５Ｄ（单位为 ｍｍ），
故公式形式变为：
Ｐ ＝ ａ（Ｑ － Ｑ ） ５Ｄ （１２）
ｓｓ ｓｓ ｓｓ
由图 ３可知，花园口站不同粒径下泥沙悬移百分比 Ｐ 均先随流量的增大而增大，增长速率呈现出
ｓｓ
先快后慢的现象，即后期增长缓慢，说明泥沙悬移百分比增加到一定程度后，继续增加变得相对困
３
难 ［３，２４］ 。粒径为 ０．０３７５ｍｍ的细颗粒泥沙当流量大于 ２０００ｍ ?ｓ时，大部分呈悬移形式输移，说明该粒
径级泥沙所受重力作用小，在水流紊动扩散作用较强时运动随机性较强，规律性变差。粒径增加后重
３
力作用逐渐增加 ［２４］ ，泥沙基本遵循相近的输移规律，在流量小于等于 ２２５０ｍ ?ｓ时，Ｐ 与流量呈幂函
ｓｓ
３
数关系，当流量大于 ２２５０ｍ ?ｓ后，Ｐ 变幅较小。粗颗粒泥沙在流量不大时多位于床面附近，受边界及
ｓｓ
３
其紊动随机性强的影响，运动规律稍显散乱。流量大于 ２０００ｍ ?ｓ后的大流量情况下，粒径 ０．０７５ｍｍ的
泥沙以悬移形式运动的比例约为 ４０％，粒径 ０．１７５ｍｍ的泥沙以悬移形式运动的比例约为 ３０％，粒径
０．３７５ｍｍ的泥沙以悬移形式运动的比例约为 １５％。总的来看，某一粒径下泥沙悬移百分比 Ｐ 与流量
ｓｓ
存在的函数关系，基本遵循式（ １２）描述的规律。
３．３ 利津站汛期泥沙输移特性 使用利津站（位于限制性弯曲型河段）２００６—２０１７年汛期数据，计算
不同粒径级下的希尔兹数和泥沙悬移百分比 Ｐ 。利津站该期间汛期均没有漫滩，流量与泥沙悬移百分
ｓｓ
比 Ｐ 的关系如图 ４所示，点据相较于花园口站的更为集中，更能遵循式（１２）描述的变化规律（利津站
ｓｓ
２
— １ ２ ４ —