Page 131 - 2022年第53卷第12期

（即 １３．８９ｈ）时）土层发生了一定程度的固结，自土层表面至土层深处可以看出孔隙水压力与孔隙气压
力的消散程度逐渐降低：如图 ８（ａ）与图 ９（ａ）所示在深度 ｚ ＝ ０ 处，孔隙水压消散比 ｕ?ｕ 为 ０，表明表
ｗ ｗ０
层土中的孔隙水压力已经完全消散，而在 ｚ ＝ ８ｍ处孔隙水压消散比 ｕ?ｕ 仍接近 １，表明在土层底部，
ｗ０
ｗ
孔隙水压力的消散程度较小。同理，在图 ８（ｂ）与图 ９（ｂ）所示孔隙气压力的消散曲线中也能看到类似
的趋势。
对比图 ８（ａ）与图 ９（ａ）所示本文解析解与文献［６］解析解的孔隙水压力消散曲线可知，这两者较为
接近，但本文解析解更接近于有限差分解的孔隙水压力消散曲线。对比图 ８（ｂ）与图 ９（ｂ）所示本文解
析解与文献［ ６］解析解的孔隙气压力消散曲线可知：由于文献［６］中将渗气系数视为常数，因此，当
２
ｔ ＝ ７．５ × １０ ｓ（即 １２．５ｍｉｎ）时，在土层底部处文献［６］解析解的孔隙气压力的消散程度还很小（其孔隙气
压消散比 ｕ?ｕ 约为 ０．９９９），但随着土层变浅，其孔隙气压力消散程度急剧增大（其孔隙气压消散比
ａ０
ａ
４
ｕ?ｕ 迅速减小至 ０）；当 ｔ ＝ ５ × １０ ｓ（即 １３．８９ｈ）时，在土层底部处文献［６］解析解的孔隙气压力消散比
ａ
ａ０
ｕ?ｕ 已经减小至不足 ０．３，随着土层变浅，孔隙气压力消散比减小至接近于 ０。相比之下，本文解析
ａ ａ０
解在考虑了渗气渗水函数后，所得的孔隙气压力消散程度较小，但在地表处这两种解析解的计算曲线
逐渐接近。
此外，由图 ８—９亦可知，本文解析解计算的的孔隙气压力消散程度高于有限差分解（图 ８（ｂ）与
图 ９（ｂ）），而其计算的孔隙水压力消散程度低于有限差分解（图 ８（ａ）与图 ９（ａ））。究其原因在于：本
文解析解在考虑渗气渗水函数的离散线性化时，对饱和度分段数的选取会显著影响考虑渗气渗水函数
的计算结果，从而使解析解计算的孔隙气、水压力的消散速率与有限差分解产生差异。
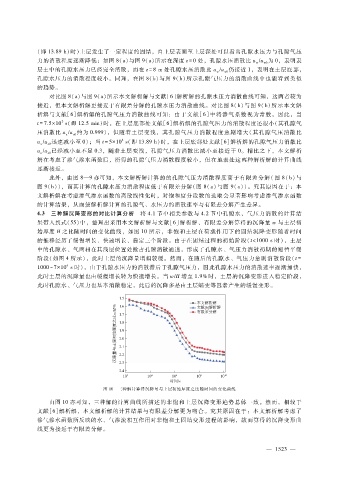
４．３ 三种解沉降变形的对比计算分析 将 ４．１节中相关参数与 ４．２节中孔隙水、气压力消散的计算结
果带入到式（５５）中，整理出采用本文解析解与文献［６］解析解、有限差分解算得的沉降量 ｗ与土层初
始厚度 Ｈ之比随时间的变化曲线，如图 １０所示，非饱和土层在荷载作用下的固结沉降变形随着时间
的推移经历了缓慢增长、快速增长、稳定三个阶段。由于在固结过程的初始阶段（ｔ＜１０００ｓ时），土层
中的孔隙水、气两相在其浅层位置处抢占孔隙消散通道，形成了孔隙水、气压力消散初期的短暂平缓
阶段（如图 ４所示），此时土层的沉降量增幅较缓。然而，在随后的孔隙水、气压力急剧消散阶段（ｔ ＝
６
１０００～７ × １０ ｓ时），由于孔隙水压力的消散滞后于孔隙气压力，因此孔隙水压力的消散速率逐渐加快，
此时土层的沉降量也由缓慢增长转为快速增长。当 ｗ?Ｈ增至 １．９％时，土层的沉降变形进入稳定阶段，
此时孔隙水、气压力也基本消散稳定，此后的沉降多是由土层蠕变等因素产生的缓慢变形。

图 １０ 三种解计算得沉降量与土层初始厚度之比随时间的变化曲线

由图 １０亦可知，三种解的计算曲线所描述的非饱和土层沉降变形趋势总体一致。然而，相较于
文献［ ６］解析解，本文解析解的计算结果与有限差分解更为吻合。究其原因在于：本文解析解考虑了
渗气渗水函数所反映的水、气渗流相互作用对非饱和土固结变形过程的影响，故而算得的沉降变形曲
线更为接近于有限差分解。

５
— １ ２ ３ —