Page 128 - 2022年第53卷第12期

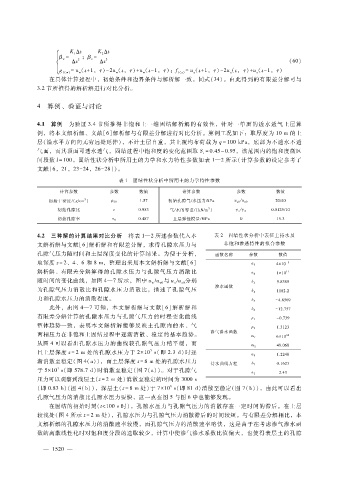
{ ＝ ＫΔ ｔ ＝ ＫΔ ｔ （６０）
１
２
β ｗ
；β ａ
２
２
Δ ｚ
Δ ｚ
ｇ ＝ｕ（ ι ＋ １，τ ） － ２ｕ（ ι ，τ ） ＋ ｕ（ ι － １，τ ）；ｆ ＝ｕ（ ι ＋ １，τ ） － ２ｕ（ ι ，τ ） ＋ ｕ（ ι － １，τ ）
１（ｗ） ｗ ｗ ｗ １（ａ） ａ ａ ａ
在具体计算过程中，初始条件和边界条件与解析解一致，同式（ ３４）。由此得到的有限差分解可与
３．２节所推得的解析解进行对比分析。
４ 算例、验证与讨论

４．１ 算例 为验证 ３．４节所推得非饱和土一维固结解析解的有效性，针对一单面的透水透气土层算
例，将本文解析解、文献［６］解析解与有限差分解进行对比分析。算例工况如下：取厚度为 １０ｍ的土
层（沿水平方向向无穷远处延伸），不计土层自重，其上覆均布荷载为 ｑ ＝ １００ｋＰａ ，底部为不透水不透
气面，而其顶面可透水透气，固结过程中饱和度的变化范围取 Ｓ＝ ０．４５～０．９５，该范围内的饱和度微区
ｒ
间段数 ｌ ＝ １００ 。固结性状分析中所用土的力学和水力特性参数如表 １—２所示（计算参数的设定参考了
文献［ ６，２１，２３ － ２４，２６ － ２８］）。

表 １ 固结性状分析中所用土的力学特性参数

计算参数 参数 数值 计算参数 参数 数值
３
初始干密度?（ｇ?ｃｍ ） ρ ｄ０ １．５７ 初始孔隙气?水压力?ｋＰａ ｕ ａ０ ?ｕ ｗ０ ２０?４０
３
初始孔隙比 ｅ ０．９５３ 气?水的容重?（ｋＮ?ｍ ） γ ａ ? γ ｗ ０．０１２５?１０
初始孔隙率 ｎ ０ ０．４８７ 土层弹性模量?ＭＰａ Ｄ １５．３

４．２ 三种解的计算结果对比分析 将表 １—２所述参数代入本 表 ２ 固结性状分析中表征土持水及
文解析解与文献［ ６］解析解和有限差分解，求得孔隙水压力与 非饱和渗透特性的拟合参数
孔隙气压力随时间和土层深度变化的计算结果。为便于分析， 函数名称 参数 数值
取深度 ｚ ＝ ２ 、４、６和 ８ｍ，整理出采用本文解析解与文献［６］ ａ ３ ４ × １０ － ５
解析解、有限差分解算得的孔隙水压力与孔隙气压力消散比 ａ ４ １ × １０ １１
随时间的变化曲线，如图 ４—７所示，图中 ｕ?ｕ 与 ｕ?ｕ 分别 ｂ ３ ９．８３８５
ｗ
ｗ０
ａ０
ａ
渗水函数
为孔隙气压力消散比和孔隙水压力消散比，描述了孔隙气压 ｂ ４ １１８２．２
力和孔隙水压力的消散程度。
ｂ ５ － ４．８５６９
此外，由图 ４—７可知，本文解析解与文献［６］解析解和
ｂ ６ － １２．７５７
有限差分解计算的孔隙水压力与孔隙气压力的时程变化曲线
ｐ １ － ０．７３９
整体趋势一致，表明本文解析解能够反映土孔隙内的水、气
ｐ ２ １．３１２３
渗气渗水函数
两相压力在非饱和土固结过程中逐渐消散、稳定的基本趋势。 ３４
ｍ １ ６ × １０
从图 ４可以看出孔隙水压力的曲线较孔隙气压力稍平缓，而
ｍ ２ ４９．０６８
５
且土层深度 ｚ ＝ ２ｍ处的孔隙水压力于 ２ × １０ ｓ（即 ２．３ｄ）时逐
ａ ５ １．２２４８
渐消散至稳定（图 ４（ａ）），而土层深度 ｚ ＝ ８ｍ处的孔隙水压力
持水曲线方程 ｂ ７ ０．１６２３
７
于 ５ × １０ ｓ（即 ５７８．７ｄ）时消散至稳定（图 ７（ａ））。对于孔隙气
ｎ １ ２．４３
压力可以观察到浅层土（ ｚ ＝ ２ｍ处）消散至稳定的时间为 ３０００ｓ
６
（即 ０．８３ｈ）（图 ４（ｂ）），深层土（ｚ ＝ ８ｍ处）于 ７ × １０ ｓ（即 ８１ｄ）消散至稳定（图 ７（ｂ）），由此可以看出
孔隙气压力的消散比孔隙水压力要快，这一点在图 ５与图 ６中也能够发现。
在固结的初始时刻（ ｔ＜１００ｓ时），孔隙水压力与孔隙气压力的消散存在一定时间的滞后。在土层
较浅处（图 ４所示 ｚ ＝ ２ｍ处），孔隙水压力与孔隙气压力消散滞后的时间较短。与有限差分解相比，本
文解析解的孔隙水压力的消散速率较慢，而孔隙气压力的消散速率略快，这是由于在考虑渗气渗水函
数的离散线性化时对饱和度分段的选取较少，计算中使渗气渗水系数比值偏大，也使得表层土的孔隙
２
— １ ５ ０ —