Page 124 - 2022年第53卷第12期

Ｓ ＝ Ｓ ＜Ｓ ＜…＜Ｓ ＝Ｓ （２２）
ｒ１ ｒ１（０） ｒ１（１） ｒ１（ｌ） ｒ２
Ｓ － Ｓ ｒ２
ｒ１
Ｓ ｒ１（ｉ ＋ １ ） － Ｓ ｒ１（ｉ） ＝ ，ｉ ＝ ０，１，２，…，ｌ － １ （２３）
ｌ
式中 ｉ为第 ｉ个饱和度微区间段。持水曲线在该微区间段内的斜率为 Ｆ ψ （ｉ） ，考虑到该值在第 ｉ个微区间
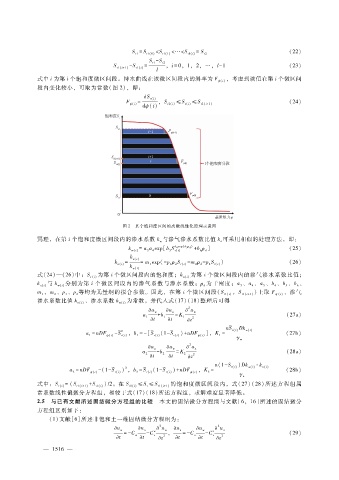
段内变化较小，可取为常数（图 ２），即：
ｄ Ｓ ｒ（ｉ）
Ｆ ＝ ，Ｓ ｒ１（ｉ） ≤Ｓ ≤Ｓ （２４）
ψ （ｉ） ｒ（ｉ） ｒ１（ｉ ＋ １）
ｄ ψ （ｉ）

图 ２ 某个饱和度区间的离散线性化原理示意图

同理，在第 ｉ个饱和度微区间段内的渗水系数 ｋ与渗气渗水系数比值 ｋ可采用相似的处理方法，即：
ｗ ｎ
ｋ ＝ａａｅｘｐ［ｂＳ ｂ ４ ｅｘｐ（ｂ ５ ρ ｄ ） ＋ ｂρ ｄ ］ （２５）
ｗ（ｉ） ３ ４ ３ ｒ（ｉ） ６
ｋ
ａ（ｉ）
ｋ ＝ ＝ｍ ｅｘｐ（ － ｐρ ｄ ｒ（ｉ） － ｐＳ ） （２６）
Ｓ － ｍ ρ ｄ
ｎ（ｉ） １ １ ２ ２ ｒ（ｉ）
ｋ
ｗ（ｉ）
式（ ２４）—（２６）中：Ｓ 为第 ｉ个微区间段内的饱和度；ｋ 为第 ｉ个微区间段内的渗气渗水系数比值；
ｒ（ｉ）
ｎ（ｉ）
为干密度；ａ、ａ、ａ、ｂ、ｂ、ｂ、
ｋ 与 ｋ 分别为第 ｉ个微区间段内的渗气系数与渗水系数；ρ ｄ ３ ４ ５ ４ ５ ６
ｗ（ｉ）
ａ（ｉ）
ｍ 、ｍ 、ｐ、ｐ等均为无量纲的拟合参数。因此，在第 ｉ个微区间段（Ｓ ｒ１（ｉ） ，Ｓ ｒ１（ｉ ＋ １ ） ）上取 Ｆ ψ（ｉ） 、渗气
１
２
１
２
渗水系数比值 ｋ 、渗水系数 ｋ 为常数，并代入式（１７）（１８）整理后可得
ｗ（ｉ）
ｎ（ｉ）
２
 ｕ ｗ  ｕ ａ ｕ ｗ
ａ １ ＋ ｂ ＝ Ｋ １ （２７ａ）
１
 ｔ  ｔ  ｚ
２
ｎ 珔 Ｄｋ
Ｓ
ｒ（ｉ）
ｗ（ｉ）
２
Ｓ
ａ＝ ｎＤＦ － 珔 ，ｂ＝－ ［ 珔 （１ － 珔 ） ＋ ｎＤＦ ］，Ｋ ＝ （２７ｂ）
Ｓ
Ｓ
１ ψ （ｉ） ｒ （ｉ） １ ｒ（ｉ） ｒ（ｉ） ψ （ｉ） １
γ ｗ
２
 ｕ ａ  ｕ ｗ ｕ ａ
ａ － ｂ ＝ Ｋ （２８ａ）
２ ２ ２ ２
 ｔ  ｔ  ｚ
ｎ（１ － 珔 ）Ｄｋ ·ｋ
Ｓ
ｒ（ｉ）
ｗ（ｉ）
ｎ（ｉ）
２
Ｓ
ａ＝ ｎＤＦ ψ （ｉ） － （１ － 珔 ），ｂ＝ 珔 （１ － 珔 ） ＋ ｎＤＦ ψ （ｉ） ，Ｋ ＝ （２８ｂ）
Ｓ
Ｓ
２
２
ｒ（ｉ）
ｒ（ｉ）
２
ｒ（ｉ）
γ ａ
式中： 珔 ＝（Ｓ ｒ１（ｉ ＋ １ ） ＋ Ｓ ｒ１（ｉ） ）?２。在 Ｓ ｒ１（ｉ） ≤Ｓ≤Ｓ ｒ１（ｉ ＋ １ ） 的饱和度微区间段内，式（２７）（２８）所述方程组属
Ｓ
ｒ（ｉ）
ｒ
常系数线性偏微分方程组，相较于式（ １７）（１８）所述方程组，求解难度显著降低。
２．５ 与已有文献所述固结微分方程组的比较 本文的固结微分方程组与文献［６，１６］所述的固结微分
方程组区别如下：
（ １）文献［６］所述非饱和土一维固结微分方程组为：
２
２
 ｕ ｗ  ｕ ａ ｕ ｗ  ｕ ａ  ｕ ｗ ｕ ａ
＝－ Ｃ － Ｃ ｗ ， ＝－ Ｃ － Ｃ ａ （２９）
２
２
 ｔ ｗ  ｔ ｖ  ｚ  ｔ ａ  ｔ ｖ  ｚ
— １ ５ ６ —
１