Page 78 - 2022年第53卷第12期

１ Ｋ（ｐ＋ ｐ）
ｆ
ａ
ｗ
Ｋ ＝ （７）
ａｗ
ｎ（ｐ＋ ｐ＋ Ｋｈ）Ｓ ＋ （１ － Ｓ）Ｋ
ｗ ａ ｆ ｆ
５
式中：ｎ为孔隙率；Ｋ为纯水的压缩模量，Ｐａ；ｐ为孔压，Ｐａ；ｐ为 １个大气压，约等于 １ × １０ Ｐａ；
ｆ ｗ ａ
Ｓ为当前饱和度；ｈ为空气在水中的体积溶解系数，一般取值 ０．０２。
随着 ｐ （等于 ｐ）的增加，水中的气泡会进一步溶解到水中，土体饱和度会逐级增大。依据 Ｂｏｙｌｅ
ａｉｒ
ｗ
定律和 Ｈｅｎｒｙ定律，孔隙气体压力变化条件下当前饱和度 Ｓ与初始饱和度 Ｓ关系可以表示为 ［２４］ ：
０
ｐ＋ ｐ
ａ
ｗ
Ｓ ＝ Ｓ ０ （８）
ｐ＋ Ｓ（１ － ｈ）ｐ
ａ ０ ｗ
（３）流固耦合方法的实现。土石坝心墙的渗透系数极小 ［１３，２５］ ，在填筑施工过程中流体渗流速度十
分缓慢，此时土与孔隙流体呈同步变形的状态 ［８］ 。根据有效应力原理，将式（１）和（４）相加，可得心
墙总应力增量与应变增量关系：
ｅｐ ｗ
ｄ σ ＝ （Ｄ ＋ Ｄ ）：ｄ ε （９）
ｗ
从上式可以看到，只需在已有的本构模型中增加 Ｄ 并记录高斯点孔压即可实现心墙孔压的分析，
并且当孔隙流体模量取 ０时，可自动退化为式（１）。由于有限元分析时外力是与总应力平衡的，因此
上式很容易在单相介质中实现，并且无需修改应力积分和迭代求解流程。更为重要的是，因本文流固
耦合方法本质是单相问题求解，因此避免了 Ｂｉｏｔ流固耦合分析矩阵病态、求解速度慢的问题。
３．２ 方法验证 基于两河口心墙坝二维有限元模型，采用 Ｂｉｏｔ流固耦合法对上述不排水流固耦合法的
适用性进行了验证。两种方法中材料参数均相同，坝体填筑过程与实际工程保持一致（共历时 ６ａ），
材料分区、填筑模拟等详细资料可见第 ４部分三维分析介绍。不排水流固耦合法中仅心墙采用不排水
方法模拟，Ｂｉｏｔ流固耦合法中心墙两侧设定为排水边界。已有研究 ［１，２６ － ２８］ 表明，试验得到渗透系数会
明显高估现场孔压的消散。为了与实际孔压累积和消散趋势保持一致，开展了不同心墙渗透系数的计
－ １０
算分析，结果表明，当渗透系数取 １ × １０ ｍ?ｓ时，计算的孔压消散发生的时间与实测时间是基本一致
－ ９
－ １０
的（见图 ５渗透系数 １ × １０ ｍ?ｓ和 １ × １０ ｍ?ｓ的 Ｂｉｏｔ流固耦合计算结果对比），因此可认为心墙的渗
－ １０
透系数是 １ × １０ ｍ?ｓ。其值明显小于试验值，这与现场心墙非饱和、封闭气泡对孔隙水以及反滤料对
细颗粒的阻滞作用有助于提高心墙的抗渗能力等因素有关。
－ １０
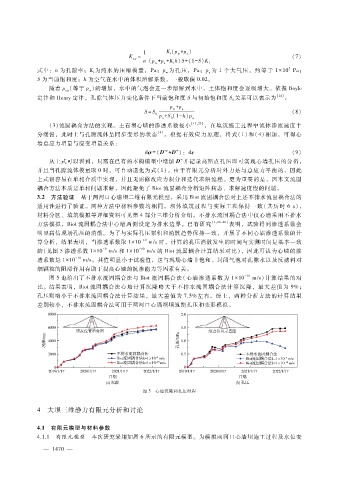
图 ５也给出了不排水流固耦合法与 Ｂｉｏｔ流固耦合法（心墙渗透系数为 １ × １０ ｍ?ｓ）计算结果的对
比。结果表明，Ｂｉｏｔ流固耦合法心墙计算沉降略大于不排水流固耦合法计算沉降，最大差值为 ９％；
孔压则略小于不排水流固耦合法计算结果，最大差值为 ７．５％左右。综上，两种分析方法的计算结果
差别较小，不排水流固耦合法可用于两河口心墙坝填筑期孔压和变形模拟。

图 ５ 心墙沉降和孔压时程

４ 大坝三维静力有限元分析和讨论

４．１ 有限元模型与材料参数
４．１．１ 有限元模型 本次研究采用如图 ６所示的有限元模型。为模拟两河口心墙坝施工过程及水位变

— １ ４ ０ —
７