Page 126 - 2023年第54卷第2期

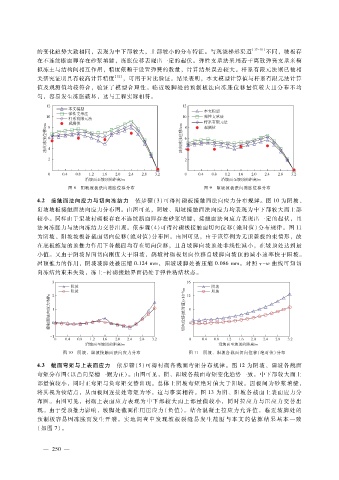
的变化趋势大致相同，表现为中下部较大，上部较小的分布特征。与现浇梯形渠道 ［１７ － １８］ 不同，坡板存
在不连续断面即存在砂浆填缝，冻胀位移表现出一定的起伏。弹性支承法采用若干离散弹簧支承来模
拟冻土与结构间相互作用，精度依赖于设置弹簧的数量，计算结果误差较大。杆系有限元法则已被相
关研究证明具有较高计算精度 ［３２］ ，可用于对比验证。结果表明，本文模型计算值与杆系有限元法计算
值及观测值均较符合，验证了模型合理性。临近坡脚处的预制板法向冻胀位移量值较大且分布不均
匀，容易发生冻胀破坏，这与工程实际相符。

图 ８ 阴坡坡板法向冻胀位移分布 图 ９ 阳坡坡板法向冻胀位移分布

４．２ 接触面法向应力与切向冻结力 依步骤（３）可得衬砌板接触面法向应力分布规律。图 １０为阴坡、
阳坡坡板接触面法向应力分布图。由图可见，阴坡、阳坡接触面法向应力均表现为中下部较大而上部
较小。同样由于渠坡衬砌板存在不连续断面即存在砂浆填缝，接触面法向应力表现出一定的起伏，且
法向冻胀力与法向冻结力交替出现。依步骤（ ４）可得衬砌板接触面切向位移（绝对值）分布规律。图 １１
为阴坡、阳坡坡板各截面切向位移（绝对值）分布图。由图可见，由于该算例为无顶盖板约束情形，故
在底板施加的顶推力作用下各截面均存在切向位移，且自坡脚向坡顶处非线性减小，在坡顶处达到最
小值。又由于阴坡界面切向刚度大于阳坡，阴坡衬砌板切向位移自坡脚向坡顶的减小速率快于阳坡。
因顶推力的作用，阴坡坡脚处被压缩 ０．１２４ｍｍ，阳坡坡脚处被压缩 ０．０８６ｍｍ。对照 τ － ｗ曲线可知切
向冻结约束未失效，冻土－ 衬砌接触界面仍处于弹性粘结状态。

图 １０ 阴坡、阳坡接触面法向应力分布 图 １１ 阴坡、阳坡各截面切向位移（绝对值）分布

４．３ 截面弯矩与上表面应力 依步骤（５）可得衬砌各截面弯矩分布规律。图 １２为阴坡、阳坡各截面
弯矩分布图（以凸向渠槽一侧为正）。由图可见，阴、阳坡各截面弯矩变化趋势一致，中下部较大而上
部量值较小，同时正弯矩与负弯矩交替出现。总体上阴坡弯矩绝对值大于阳坡。因板间为砂浆填缝，
将其视为铰结点，从而板间连接处弯矩为零，这与事实相符。图 １３为阴、阳坡各截面上表面应力分
布图。由图可见，衬砌上表面应力表现为中下部较大而上部量值较小，同时拉应力与压应力交替出
现。由于受顶推力影响，坡脚处截面作用压应力（负值）。结合混凝土拉应力允许值，临近坡脚处的
预制板容易因冻胀而发生 开裂。实地 调查中 发现坡板裂 缝易 发生 范围 与本 文 的 估 算 结 果 基 本 一 致
（如图 ７）。

０
— ２ ５ —