Page 121 - 2023年第54卷第2期

类模型的计算结果是偏保守的，尤其是对板间填缝的处理不完全符合实际。
渠道冻胀力学分析结构力学模型发展已较充分。王正中等 ［８ － ９］ 等对现浇梯形、弧底梯形渠道，宋
玲等 ［１０］ 对冬季输水梯形渠道，唐少容等 ［１１］ 对三拼式 Ｕ形渠道，葛建锐等 ［１２］ 等对冰盖输水梯形渠道，
肖等 ［１３］ 对弧底浅拱梯形渠道分别构建冻胀力学模型。但此类模型仍未考虑冻土 － 结构间的相互作
用。弹性地基梁模型因其能较好地描述土体 － 结构间相互作用与协调变形，在各类寒区工程力学分析
中得到广泛应用 ［１４ － １６］ 。就渠道而言，肖等 ［１７］ 引入与冻胀变形成比例的附加项来描述冻胀力随冻胀
变形的释放与衰减现象，构建考虑冻土 － 结构相互作用的现浇梯形渠道弹性冻土地基梁模型。李宗利
等 ［１８］ 类比常温土地基沉降模型中的 “基床系数” 引入 “冻胀力系数” 的概念，建立可与规范 ［１９］ 计算
成果相衔接的梯形渠道冻胀破坏弹性地基梁模型。何鹏飞等 ［２０］ 考虑切向冻结力的影响建立弹性地基梁
模型的控制方程对文献［ １７］模型进行了修正，指出校核衬砌板的强度时宜考虑切向冻结力的影响，但
其忽略了衬砌板自身变形引起的接触面应力，江浩源等 ［２１］ 基于此做了进一步修正。葛建锐等 ［２２］ 提出
了考虑冰盖生消及冰－ 结构－ 冻土协同作用的冰盖输水工况梯形渠道弹性地基梁模型。为此本文在现有
模型基础上，基于 Ｗｉｎｋｌｅｒ理论 ［２３ － ２４］ ，考虑冻土 － 衬砌结构间及预制板间相互作用与协调变形，构建
预制混凝土衬砌梯形渠道弹性冻土地基梁模型。

２ 模型构建

２．１ 基本假设 结合已有研究及工程实践 ［８ － ９］ ，作如下假设：
（１）以预制板铺设数量以及尺寸均适中的预制混凝土衬砌砂浆填缝梯形渠道为研究对象。不考虑
预制块的情形，即暂不考虑铺设数量较多同时单块尺寸显著小于断面尺寸的情形 ［６ － ７］ 。同时不失一般
性，假设渠坡与渠底均铺设 ｎ块预制板。忽略砂浆填缝的缝宽。
（２）渠基冻土满足 Ｗｉｎｋｌｅｒ假设，如图 １。参考李宗利等 ［１８］ 的研究，用法向 Ｗｉｎｋｌｅｒ弹簧的伸缩变形
反映基土法向变形。为便于衔接规范 ［１９］ ，以基土天然冻胀量为弹簧原长，且只考虑均匀冻胀情形。因衬
砌端部受约束，使各点不能同步冻胀变形，导致土弹簧无法到达原长而引起的反力视为法向冻胀力。冻
土－ 衬砌接触界面有脱离趋势时，土弹簧伸长引起的反力视为法向冻结力。两者合称接触面法向应力。

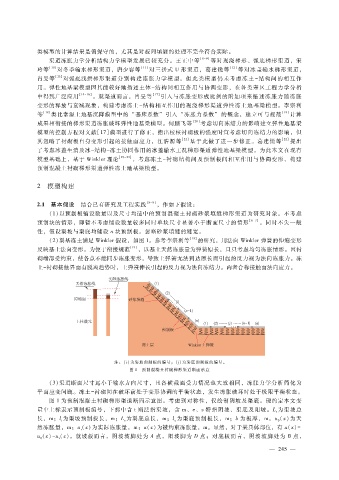
注：（ｉ）为渠坡预制板的编号；（ｊ）为渠底预制板的编号。
图 １ 预制混凝土衬砌梯形渠道断面示意
（３）渠道断面尺寸远小于输水方向尺寸，且各横截面受力情况也大致相同，冻胀力学分析简化为
平面应变问题。冻土－ 衬砌间在破坏前处于变形协调的平衡状态，发生冻胀破坏时处于极限平衡状态。
图 １为预制混凝土衬砌梯形渠道断面示意图。考虑到对称性，仅绘制阴坡及渠底。现约定本文变
量中上标表示预制板编号，下标中含 ｔ则泛指渠坡，含 ｍ、ｅ、ｓ特指阴坡、渠底及阳坡。Ｌ为渠坡总
ｔ
长，ｍ；ｌ为渠坡预制板长，ｍ；Ｌ为渠底总长，ｍ；ｌ为渠底预制板长，ｍ；ｂ为板厚，ｍ。ｕ（ｘ）为天
０
ｅ
ｅ
ｔ
然冻胀量，ｍ；ｕ（ｘ）为实际冻胀量，ｍ；ｕ（ｘ）为被约束冻胀量，ｍ。显然，对于某具体部位，有 ｕ（ｘ） ＝
ｒ
ｕ（ｘ） － ｕ（ｘ）。就坡板而言，阴坡坡脚处为 Ａ点，阳坡脚为 Ｄ点；对底板而言，阴坡坡脚处为 Ｂ点，
０
ｒ
— ２ ４ ５ —