Page 67 - 2023年第54卷第2期

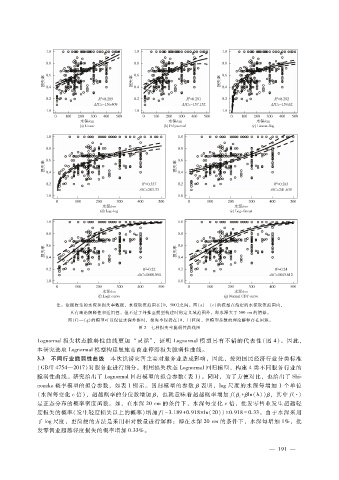
注：依据收集的水深和损失率数据，水深取值范围在［０，５００］之间。图（ａ）—（ｅ）的模型在给定的水深取值范围内，
具有理论解释性和适用性，但不适于外推至模型构建时的定义域范围外，即水深大于 ５００ｃｍ的情景。
图（ ｆ）—（ｇ）的模型可以保证水深外推时，损失率保持在［０，１］区间，但模型参数的理论解释存在困难。
图 ２ 七种损失率脆弱性曲线图

Ｌｏｇｎｏｒｍａｌ损失状态脆弱性曲线更加 “灵活”，证明 Ｌｏｇｎｏｒｍａｌ模型具有不错的代表性（图 ４）。因此，
本研究选取 Ｌｏｇｎｏｒｍａｌ模型构建恩施市商业停滞损失脆弱性曲线。
３．３ 不同行业脆弱性曲线 本次洪涝灾害主要对服务业造成影响，因此，按照国民经济行业分类标准
（ ＧＢ?Ｔ４７５４—２０１７）对服务业进行细分。利用损失状态 Ｌｏｇｎｏｒｍａｌ回归模型，构建 ４类不同服务行业的
脆弱性曲线。研究给出了 Ｌｏｇｎｏｒｍａｌ回归模型的拟合参数（表 １）。同时，为了方便对比，也给出了 Ｓｈｉ
ｎｏｚｕｋａ概率模型的拟合参数，如表 １所示。回归模型的参数 β表明，ｌｏｇ尺度的水深每增加 １个单位
＋
（水深每变化 ｅ倍），超越概率的分位数增加 β ，也就意味着超越概率增加 ｆ（ β ｉ β ｌｎ（ｈ）） β ，其中 ｆ（·）
是正态分布的概率密度函数。如，在水深 ２０ｃｍ的条件下，水深每变化 ｅ倍，批发零售业发生超越轻
度损失的概率（发生轻度损失以上的概率）增加 ｆ（ － ３．１８９ ＋ ０．９１８ × ｌｎ（２０）） × ０．９１８ ＝ ０．３３。由于水深采用
了 ｌｏｇ尺度，更简便的方法是采用相对数量进行解释：即在水深 ２０ｃｍ的条件下，水深每增加 １％，批
发零售业超越轻度损失的概率增加 ０．３３％。

— １ ９ １ —