Page 66 - 2023年第54卷第2期

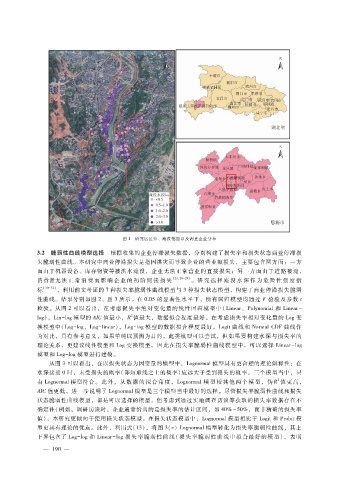
图 １ 研究区区位、淹没范围以及调查企业分布

３．２ 脆弱性曲线模型选择 根据收集的企业停滞损失数据，分别构建了损失率和损失状态商业停滞损
失脆弱性曲线。本研究中商业停滞损失是指因洪灾而导致企业的营业额损失，主要包含两方面：一方
面由于机器设备、库存物资等被洪水淹没，企业无法正常营业的直接损失；另一方面由于道路被淹，
消费者无 法 正 常 消 费 而 影 响 企 业 的 初 阶 间 接 损 失 ［２３，２８ － ２９］ 。 研 究 选 择 淹 没 水 深 作 为 危 险 性 强 度 指
标 ［３０ － ３２］ ，利用前文考证的 ７种损失率脆弱性曲线模型与 ３种损失状态模型，构建了商业停滞损失脆弱
性曲线。结果分别如图 ２、图 ３所示。在 ０．０５的显著性水平下，所有回归模型均通过 Ｆ检验及参数 ｔ
检验。从图 ２可以看出，在考虑损失率绝对变化量的线性回归模型中（Ｌｉｎｅａｒ、Ｐｏｌｙｎｏｍｉａｌ和 Ｌｉｎｅａｒ －
２
ｌｏｇ），Ｌｉｎ － ｌｏｇ模型的 ＡＩＣ值最小，Ｒ值最大，数据拟合程度最好。在考虑损失率相对变化量的 Ｌｏｇ变
换模型中（Ｌｏｇ － ｌｏｇ、Ｌｏｇ － ｌｉｎｅａｒ），Ｌｏｇ － ｌｏｇ模型的数据拟合程度最好。Ｌｏｇｉｔ曲线和 ＮｏｒｍａｌＣＤＦ曲线作
为对比，具有参考意义，如果单纯以预测为目的，此类模型可以尝试，但如果要构建水深与损失率的
理论关系，更建议线性模型和 Ｌｏｇ变换模型。因此在损失率脆弱性曲线模型中，可以选择 Ｌｉｎｅａｒ － ｌｏｇ
模型和 Ｌｏｇ － ｌｏｇ模型进行建模。
从图 ３可以看出，在以损失状态为因变量的模型中，Ｌｏｇｎｏｒｍａｌ模型具有更合理的理论解释性：在
水深接近 ０时，未受损失的概率（即短虚线之上的概率）应远大于受到损失的概率。三个模型当中，只
２
有 Ｌｏｇｎｏｒｍａｌ模型符 合。此 外，从 数 据 的 拟 合 角 度，Ｌｏｇｎｏｒｍａｌ模 型 较 其 他 两 个 模 型，伪 Ｒ 值 更 高，
ＡＩＣ值更低，进一步说明了 Ｌｏｇｎｏｒｍａｌ模型是三个模型当中最好的选择。尽管损失率脆弱性曲线和损失
状态脆弱性曲线模型，都是可以选择的模型，但考虑到通过实地调查访谈等获取的损失率数据存在不
确定性（例如，调研访谈时，企业通常给出的是损失率的估计区间，如 ４０％～５０％，而非精确的损失率
值），本研究更倾向于使用损失状态模型。在损失状态模型中，Ｌｏｇｎｏｒｍａｌ模型相比于 Ｌｏｇｉｔ和 Ｐｒｏｂｉｔ模
型更具有理论的优点。此外，利用式（ １３），将图 ３（ｃ）Ｌｏｇｎｏｒｍａｌ模型转化为损失率脆弱性曲线，其上
下界包含了 Ｌｏｇ － ｌｏｇ和 Ｌｉｎｅａｒ － ｌｏｇ损失率脆弱性曲线（损失率脆弱性曲线中拟合最好的模型），表明

— １ ９ —
０