Page 25 - 2023年第54卷第5期


卸料开始时间误差和结束时间误差计算如式（９）（１０）所示，式中 Ｔ＿ｓｔａｒｔ为真实的卸料开始时间，

Ｔ＿ｅｎｄ 为真实的卸料结束时间。在测试视频中累计判断出 １３６次卸料，其中每车次的卸料开始时间和
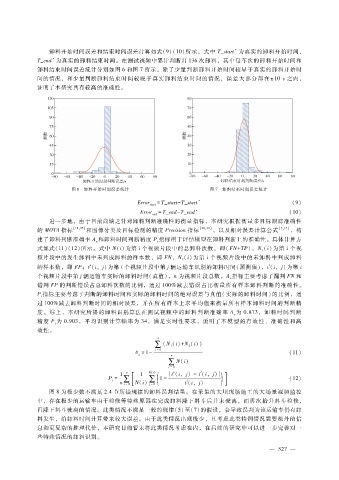
卸料结束时间误差统计分别如图 ６和图 ７所示。除了少量判断卸料开始时间较早于真实的卸料开始时
间的情况，和少量判断卸料结束时间较晚于真实卸料结束时间的情况，误差大部分都在 ±１０ｓ之内，
证明了本研究具有较高的准确性。

图 ６ 卸料开始时间误差统计 图 ７ 卸料结束时间误差统计


Ｅｒｒｏｒ ＝ Ｔ＿ｓｔａｒｔ － Ｔ＿ｓｔａｒｔ （９）
ｓｔａｒｔ
Ｅｒｒｏｒ ＝ Ｔ＿ｅｎｄ － Ｔ＿ｅｎｄ  （１０）
ｅｎｄ
进一步地，由于目前尚缺乏针对卸料判断准确性的衡量指标，本研究根据衡量多目标跟踪准确性
的 ＭＯＴＡ指标 ［１８，２５］ 和图像分类及目标检测的精度 Ｐｒｅｃｉｓｉｏｎ指标 ［２８，３２］ ，以及相对误差计算公式 ［５，１５］ ，构
建了卸料判断准确率 Ａ和卸料时间判断精度 Ｐ指标用于评估模型在卸料判断上的准确性。具体计算方
ｕ
ｔ
式如式（１１）（１２）所示。式中 Ｎ（ｉ）为第 ｉ个视频片段中的总卸料次数，即（ＦＮ ＋ ＴＰ），Ｎ（ｉ）为第 ｉ个视
１
频片段中的发生卸料中未判成卸料的样本数，即 ＦＮ，Ｎ（ｉ）为第 ｉ个视频片段中的未卸料中判成卸料
２
ｐ
ｌ
的样本数，即 ＦＰ；ｔ（ｉ，ｊ）为第 ｉ个视频片段中第 ｊ辆运输车识别的卸料时间（预测值），ｔ（ｉ，ｊ）为第 ｉ
个视频片段中第 ｊ辆运输车实际的卸料时间（真值），ｎ为视频片段总数。Ａ指标主要考虑了漏判 ＦＮ和
ｕ
错判 ＦＰ的判断错误占总卸料次数的比例，通过 １００％减去错误占比衡量所有样本卸料判断的准确性。
Ｐ指标主要考虑了判断的卸料时间和实际的卸料时间的绝对误差与真值（实际的卸料时间）的比例，通
ｔ
过 １００％减去卸料判断时间的相对误差，并在所有样本上求平均值来衡量所有样本卸料时间的判断精
度。综上，本研究所提的卸料识别算法在测试视频中的卸料判断准确率 Ａ为 ０．８７３，卸料时间判断
ｕ
精度 Ｐ为 ０．９０３，平均识别计算帧率为 ３４，满足实时性要求，说明了本模型的有效性、准确性和高
ｔ
效性。
ｎ
∑ （Ｎ（ｉ） ＋ Ｎ（ｉ））
２
１
Ａ ＝ １ － ｉ ＝０ ｎ （１１）
ｕ
∑ Ｎ（ｉ）
ｉ ＝０
ｐ
ｌ
１ ｎ １ Ｎ（ｉ） ｔ（ｉ，ｊ）－ｔ （ｉ，ｊ）
１ －
ｔ ∑
Ｐ＝ [ ∑( ｌ )] （１２）
ｎ ｉ ＝０ Ｎ（ｉ） ｊ ＝０ ｔ（ｉ，ｊ）
图 ８为极少数不满足 ２．４节所提规律的卸料误判结果。在采集的大坝现场施工的大场景视频监控
中，存在极少的运输车由于检修等特殊原因在完成卸料降下料斗后并未驶离，而再次抬升料斗检修，
再降下料斗驶离的情况。此类情况不满足一般的规律（ ５）至（７）的假设，会导致误判为该运输车仍有卸
料发生，给卸料时间计算带来较大误差。由于此类情况出现极少，且考虑此类特例情况需要额外的信
息和更复杂的推理代价，本研究目前暂未将此类情况考虑在内，在后续的研究中可以进一步完善对一
些特殊情况的卸料识别。

— ５ ２ ７ —