Page 7 - 2023年第54卷第5期

目标函数或约束条件随时间变化。此外，面临复杂的实际调度情况时，上述几种变化类型在调度期内
可能会同时发生，但研究中一般仅考虑前三种变化类型。

图 ２ 动态两目标优化问题示意图

３ 防洪库容置换

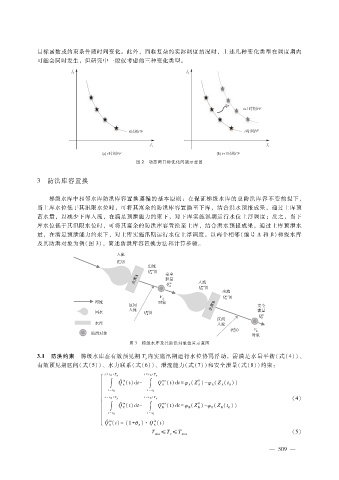
梯级水库中相邻水库防洪库容置换遵循的基本原则：在保证梯级水库的总防洪库容不变前提下，
当上库水位低于其汛限水位时，可将其富余的防洪库容置换至下库，结合洪水预报成果，通过上库预
蓄水量，以减少下库入流，在满足预泄能力约束下，对下库实施汛期运行水位上浮调度；反之，当下
库水位低于其汛限水位时，可将其富余的防洪库容置换至上库，结合洪水预报成果，通过上库预泄水
量，在满足预泄能力约束下，对上库实施汛期运行水位上浮调度。以两个相邻（编号 Ａ和 Ｂ）梯级水库
及其防洪对象为例（图 ３），简述防洪库容置换方法和计算步骤。

图 ３ 梯级水库及其防洪对象位置示意图

３．１ 防洪约束 梯级水库在有效预见期 Ｔ内实施汛期运行水位协同浮动，需满足水量平衡（式（４））、
ｙ
有效预见期区间（式（５））、水力联系（式（６））、泄流能力（式（７））和安全泄量（式（８））约束：
ｔ ＝ ｔ ０ ＋ Ｔ ｙ ｔ ＝ ｔ ０ ＋ Ｔ ｙ
＾
ｉｎ
Ｑ （ｔ）ｄｔ － ｏｕｔ ０ （Ｚ（ｔ））
Ａ
Ｑ （ｔ）ｄｔ ＝ φ Ａ
∫ Ａ ∫ Ａ （Ｚ ） － φ Ａ Ａ ０
ｔ ＝ ｔ ０ ｔ ＝ ｔ ０
（ ４）
ｔ ＝ ｔ ０ ＋ Ｔ ｙ ｔ ＝ ｔ ０ ＋ Ｔ ｙ
＾
ｉｎ
Ｑ （ｔ）ｄｔ － ｏｕｔ ０ （Ｚ（ｔ））
Ｑ （ｔ）ｄｔ ＝ φ Ｂ
∫ Ｂ ∫ Ｂ （Ｚ ） － φ Ｂ Ｂ ０
Ｂ
ｔ ＝ ｔ ０ ｔ ＝ ｔ ０
＾ ｉｎ
ｉｎ
Ａ Ａ
Ｑ （ｔ） ＝（１ ＋ θ Ａ ）·Ｑ （ｔ）
Ｔ ≤Ｔ≤Ｔ ｍａｘ （５）
ｍｉｎ
ｙ
— ５ ０ ９ —