Page 78 - 2023年第54卷第5期

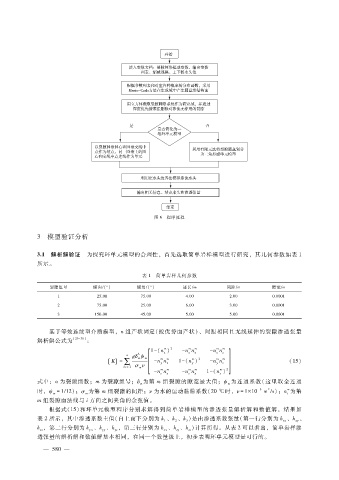
图 ６ 程序流程

３ 模型验证分析

３．１ 解析解验证 为探究环单元模型的合理性，首先选取简单岩样模型进行研究，其几何参数如表 １
所示。

表 １ 简单岩样几何参数
裂隙组号 倾向?（°） 倾角?（°） 迹长?ｍ 间距?ｍ 隙宽?ｍ
１ ２５．００ ７５．００ ４．００ ２．００ ０．０００１
２ ７５．００ ２５．００ ６．００ ３．００ ０．０００１
３ １５０．００ ４５．００ ５．００ ５．００ ０．０００１

基于等效连续型介质模型，ｎ组产状固定（按优势面产状）、间距相同且无线延伸的裂隙渗透张量
解析解公式为 ［２９ － ３０］ ：
ｍ
ｍ
ｍ
１ － （ｎ） ２ － ｎｎ ｍ － ｎｎ ｍ
ｎ ３ ｘ ｘ ｙ ｘ ｚ
ｇ δ ｍ ψ ｍ ｍ ｍ ｍ ２ ｍ ｍ
[ Ｋ ] ＝ ∑ － ｎｎ ｘ １ － （ｎ） － ｎｎ ｚ （１５）
ｙ
ｙ
ｙ
ｍ＝１ σ ｍ ν
ｍ
ｍ
ｍ
－ ｎｎ ｍ － ｎｎ ｍ １ － （ｎ） ２
ｚ ｘ ｚ ｙ ｚ
为连通系数（这里取全连通
式中：ｎ为裂隙组数；ｍ为裂隙组号；δ ｍ 为第 ｍ组裂隙的隙宽最大值；ψ ｍ
ｍ
－ ６
２
为第 ｍ组裂隙的间距；ν 为水的运动黏滞系数（２０℃时，ν ＝ １ × １０ ｍ ?ｓ）；ｎ为第
时，ψ ｍ ＝ １?１２ ）；σ ｍ ｉ
ｍ组裂隙面法线与 ｉ方向之间夹角的余弦值。
根据式（ １５）和环单元模型程序分别求解得到简单岩样模型的渗透张量解析解和数值解，结果如
表 ２所示，其中渗透系数主值（自上而下分别为 ｋ、ｋ、ｋ）是由渗透系数张量（第一行分别为 ｋ 、ｋ 、
ｘｘ
ｘｙ
３
２
１
ｋ，第二行分别为 ｋ 、ｋ 、ｋ，第三行分别为 ｋ 、ｋ、ｋ）计算所得。从表 ２可以看出，简单岩样渗
ｙｘ
ｙｚ
ｙｙ
ｚｙ
ｚｘ
ｘｚ
ｚｚ
透张量的解析解和数值解基本相同，在同一个数量级上，初步表明环单元模型是可行的。
— ５ ８ —
０