Page 80 - 2023年第54卷第5期

数及主方向与面单元模型计算得到的渗透主系数及主方向都相差不大。综上，环单元模型是可行的，
计算精度优于面单元模型。虽然环单元模型是基于面状流模型上的简化模型，精度确实不应该高于面
状流模型，但从宏观上讲，我们可能无法完全地模拟出来自然界中的裂隙，文中之所以造成环单元模
型精度高于面状流模型的现象，可能有以下几个原因：（ １）两模型在表征单元体选取上产生的误差；
（ ２）文中裂隙是按光滑平行板模型处理的，可能造成近似误差，导致整体反映不全面；（３）文中并未考
虑裂隙粗糙度因素的影响。在大小相同的研究域内，环单元模型产生的结点数和单元数明显少于面单
元模型产生的，工程中为了减小渗透张量的计算规模，可优先选择环单元模型。
表 ４ 岩样在不同解法下的渗透张量

渗透系数主值 主轴方位?（°）
计算方法 渗透系数张量?（ｍ?ｓ）
?（ｍ?ｓ） 倾向 倾角
４．６０ × １０ － ７ １．９１ × １０ － ８ ２．１０ × １０ － ８ ３．０８ × １０ － ７ １７０．０ １９．８
现场压水试验 １．９１ × １０ － ８ ３．２６ × １０ － ７ － ３．９１ × １０ － ８ ４．３３ × １０ － ７ ４５．９ ５７．３
２．１０ × １０ － ８ － ３．９１ × １０ － ８ ４．２５ × １０ － ７ ４．７０ × １０ － ７ ２６９．６ ２４．８
－ ７ － ８ － ７ － ７
４．５６ × １０ ６．１１ × １０ １．１４ × １０ ２．９０ × １０ １４０．２ １８．４
环单元 ６．１１ × １０ － ８ ３．２１ × １０ － ７ － ８．０５ × １０ － ９ ４．３２ × １０ － ７ ４３．６ ５５．７
－ ７ － ９ － ７ － ７
１．１４ × １０ － ８．０５ × １０ ５．２５ × １０ ５．８０ × １０ １１５．０ １１２．３
－ ７ － ８ － ８ － ７
６．１０ × １０ １．２７ × １０ ９．４３ × １０ ２．０１ × １０ １６０．９ ３２．７
面单元 １．２７ × １０ － ８ ２．６０ × １０ － ７ ３．８７ × １０ － ８ ２．８０ × １０ － ７ １１．３ ６１．１
９．４３ × １０ － ８ ３．８７ × １０ － ８ ２．４４ × １０ － ７ ６．３４ × １０ － ７ ９３．４ １０３．９

表 ５ 三组渗透主值之间的误差

分组 现场压水试验 环单元 面单元 误差
＝
＝
＝
＝
＝
＝
１ √ √ ○ ε １ ０．０５８４ ，θ １ ８６．３° ；ε ２ ０．００２３ ，θ ２ ８８．４° ；ε ３ ０．２３４０ ，θ ３ ５３．２°
＝
＝
＝
＝
＝
＝
２ √ ○ √ ε １ ０．３４７４ ，θ １ ８０．９° ；ε ２ ０．３５３３ ，θ ２ ８１．３° ；ε ３ ０．３４８９ ，θ ３ １１．３°
＝
＝
＝
＝
＝
＝
３ ○ √ √ ε １ ０．３０６９，θ １ ２７．６°；ε ２ ０．３５１９，θ ２ ４６．５°；ε ３ ０．０９３１，θ ３ ４５．６°
注：√表示选取，○表示未选取。
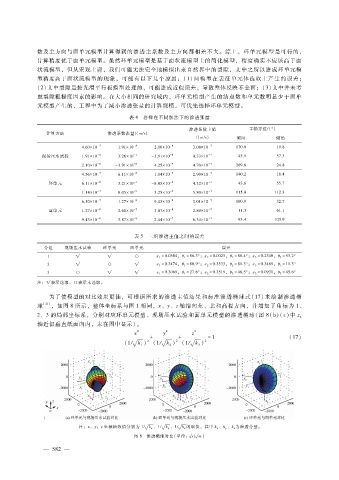
为了使模型的对比效果更佳，可根据所求的渗透主值结果和标准渗透椭球式（１７）来绘制渗透椭
球 ［２１］ ，如图 ８所示，整体坐标系与图 １相同，ｘ、ｙ、ｚ轴指向东、北和高程方向，并增加了角标为 １、
２、３的局部坐标系，分别对应环单元模型、现场压水试验和面单元模型的渗透椭球（图 ８（ｂ）（ｃ）中 ｚ
３
轴近似垂直纸面向内，未在图中显示）。
２
２
２
ｘ ｙ ｚ
＋ ＋ ＝ １ （１７）
２
２
（１? ｋ） （１? ｋ） （１? ｋ） ２
槡
槡
槡
２
３
１
注：ｘ，ｙ，ｚ坐标轴数值分别为 １? ｋ ｘ 、１? ｋ ｙ 、１? ｋ ｚ 的取值，其中 ｋ ｘ 、ｋ ｙ 、ｋ ｚ 为渗透分量。
槡 槡 槡
图 ８ 渗透椭球对比（单位： ｓ?ｍ）
槡 槡
２
— ５ ８ —