Page 75 - 2023年第54卷第5期

２．２ 环单元模型的建立
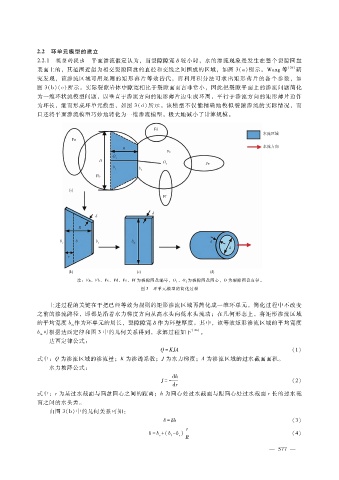
２．２．１ 模型的提出 平面渗流假定认为，当裂隙隙宽 δ 较小时，水的渗流现象是发生在整个裂隙圆盘
表面上的，其范围近似为相交裂隙圆盘的直径和交线之间围成的区域，如图 ３（ａ）所示。Ｗａｎｇ等 ［２６］ 研
究发现，该渗流区域可用规则的矩形薄片等效替代，再利用积分法可求出矩形薄片的各个参数，如
图 ３（ｂ）（ｃ）所示。实际裂隙岩体中隙宽相比于裂隙面而言非常小，因此把裂隙平面上的渗流问题简化
为一维环状流模型问题，以垂直于渗流方向的矩形薄片边生成环周，平行于渗流方向的矩形薄片边作
为环长，继而形成环单元模型，如图 ３（ｄ）所示。该模型不仅能精确地模拟裂隙渗流的实际情况，而
且还将平面渗流模型巧妙地转化为一维渗流模型，极大地减小了计算规模。

注：Ｆａ、Ｆｂ、Ｆｃ、Ｆｄ、Ｆｅ、Ｆｆ为裂隙圆盘编号，Ｏ １ 、Ｏ ２ 为裂隙圆盘圆心，Ｄ为裂隙圆盘直径。
图 ３ 环单元模型的简化过程

上述过程的关键在于把已经等效为规则的矩形渗流区域再简化成一维环单元，简化过程中不改变
之前的渗流路径，即都是沿着水力梯度方向从高水头向低水头流动；在几何形态上，将矩形渗流区域
的平均宽度 ｂ作为环单元的周长，裂隙隙宽 δ 作为环壁厚度。其中，该等效矩形渗流区域的平均宽度
ｍ
ｂ可根据达西定律和图 ３中的几何关系得到，求解过程如下 ［２６］ 。
ｍ
达西定律公式：
Ｑ ＝ ＫＪＡ （１）
式中：Ｑ为渗流区域的渗流量；Ｋ为渗透系数；Ｊ为水力梯度；Ａ为渗流区域的过水截面面积。
水力坡降公式：
ｄ ｈ
Ｊ ＝－ （２）
ｄｒ
式中：ｒ为某过水截面与圆盘圆心之间的距离；ｈ为圆心处过水截面与距圆心处过水截面 ｒ长的过水截
面之间的水头差。
由图 ３（ｂ）中的几何关系可知：
Ａ ＝ δ ｂ （３）
ｒ
ｂ ＝ ｂ＋ （ｂ － ｂ） （４）
ｃ ｌ ｃ
Ｒ
— ５ ７ ７ —