Page 79 - 2023年第54卷第5期

表 ２ 简单岩样模型求解结果对比
渗透系数主值 主轴方位?（°）
计算方法 渗透系数张量?（ｍ?ｓ）
?（ｍ?ｓ） 倾向 倾角
－ ７ － ８ － ７ － ７
７．９７ × １０ － ９．９９ × １０ － １．３６ × １０ １．８６ × １０ ２０４．８ ５０．６
解析解 － ９．９９ × １０ － ８ ５．０５ × １０ － ７ － ２．０４ × １０ － ７ ６．５８ × １０ － ７ ０．５ ３６．６
－ １．３６ × １０ － ７ － ２．０４ × １０ － ７ ３．８５ × １０ － ７ ８．４３ × １０ － ７ ９９．１ １２．５
７．１１ × １０ － ７ ２．３６ × １０ － ７ ２．０９ × １０ － ７ ３．３２ × １０ － ７ ３３１．５ ７．３
环单元 ２．３６ × １０ － ７ ４．７４ × １０ － ７ ９．５４ × １０ － ８ １．３２ × １０ － ７ ８３．１ ７０．９
２．０９ × １０ － ７ ９．５４ × １０ － ８ ２．０８ × １０ － ７ ９．２９ × １０ － ７ ２３９．２ １７．６

３．２ 实例验证 通过实例岩体继续对环单元模型的合理性进行验证，选取的裂隙岩体结构面参数见李
新强等 ［３１］ 实测得到的统计表（表 ３）。
表 ３ 岩样实测参数
结构面分组
统计指标类型 １ ２ ３ 概率分布类型
均值 标准差 均值 标准差 均值 标准差
倾向?（°） ０．００ １０．００ ７５．００ １５．００ １５０．００ １０．００ 正态
倾角?（°） ９０．００ １０．００ ２５．００ １５．００ ４５．００ １０．００ 正态
迹长?ｍ ４．００ ４．００ ６．００ ６．００ ５．００ ５．００ 负指数
间距?ｍ ２．００ ２．００ ３．００ ３．００ ５．００ ５．００ 负指数
隙宽?ｍ ０．０００１ ０．０００１ ０．０００１ ０．０００１ ０．０００１ ０．０００１ 对数正态

针对该裂隙岩体，设定自编译的渗透张量程序参数如
下：生成域的大小为 １０ｍ × １０ｍ × １０ｍ，研究域的大小为
６ｍ × ６ｍ × ６ｍ，定水头边界的水头大小为 Ｈ ＝ ３０ｍ 、Ｈ ＝
１ ２
１０ｍ 。运行程序，计 算模 型采 用环单 元模 型，校核模型
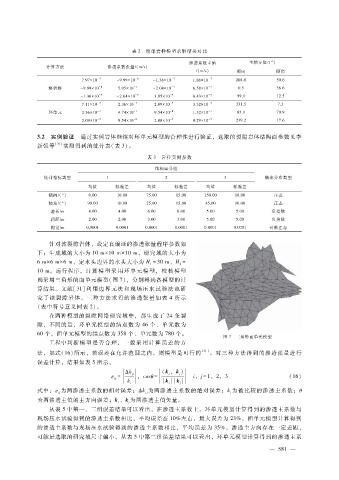
则采用三角形的面单元模型（图 ７），分别得到各模型的计
算结果。文献［ ３１］利用边界元法和现场压水试验法也研
究了该裂隙岩体。三种方法求得的渗透张量如表 ４所示
（表中符号意义同表 ２）。
在两种模型的裂隙网络研究域中，都生成了 ２４条裂
隙，不同的是，环单元模型的结点数为 ４６个、单元数为
６０个，面单元模型的结点数为 ３５８个、单元数为 ７８０个。
图 ７ 三角形面单元模型
工程中判断模型是否合理，一般采 用 计算 误 差的方
法，如式（ １６）所示，若误差在允许范围之内，则模型是可行的 ［２１］ 。对三种方法得到的渗透张量进行
误差计算，结果如表 ５所示。
Δ ｋ ｉｊ （ｋ，ｋ）
ｉ
ｊ
＝ ，ｃｏｓ θ ＝ ｉ，ｊ ＝ １ ，２，３ （１６）
ε ｉｊ
ｋ ｋ ｉ ｋ ｊ
ｉ
为两渗透主系数的相对误差；Δ ｋ为两渗透主系数的绝对误差；ｋ为被比较的渗透主系数；θ
式中：ε ｉｊ ｉｊ ｉ
为两渗透主值的主方向误差；ｋ、ｋ为两渗透主值矢量。
ｉ ｊ
从表 ５中第一、二组误差结果可以看出，在渗透主系数上，环单元模型计算得到的渗透主系数与
现场压水试验得到的渗透主系数相比，平均误差在 １０％左右，最大误差为 ２３％，面单元模型计算得到
的渗透主系数与现场压水试验得到的渗透主系数相比，平均误差为 ３５％，渗透主方向存在一定差距，
可能是选取的研究域尺寸偏小。从表 ５中第三组误差结果可以看出，环单元模型计算得到的渗透主系

— ５ ８ １ —