Page 70 - 2023年第54卷第5期
P. 70
表 3 黄河下游土城子河段典型挟沙观测资料检验与比较
S? V? 舒安平 张红武
序号 h?m J? n ω ?(cm?s) d 50 ?mm D 50 ?mm f m 因子 2
3
(kg?m ) (m?s) 公式 (1991)公式
1 3.69 0.74 0.96 1.40 0.016 0.158 0.02 0.080 0.0193 799.76 1.19 3.68
2 3.96 0.85 1.74 0.92 0.016 0.134 0.02 0.070 0.0174 850.07 1.13 3.86
3 3.88 0.97 1.65 0.94 0.014 0.160 0.02 0.060 0.0129 1020.11 0.99 4.61
4 5.88 0.92 1.75 0.96 0.015 0.112 0.01 0.067 0.0156 1202.86 1.42 5.00
5 10.4 1.40 1.50 1.10 0.010 0.092 0.01 0.077 0.0066 4100.62 1.92 13.25
6 9.84 1.58 1.45 1.10 0.009 0.118 0.01 0.073 0.0050 4473.75 1.55 14.59
7 9.27 1.79 1.91 0.97 0.008 0.128 0.02 0.071 0.0045 4753.23 1.48 15.08
8 12.1 1.52 1.41 1.30 0.009 0.103 0.01 0.076 0.0062 5075.14 2.23 14.95
9 12.6 1.52 1.46 1.20 0.009 0.093 0.01 0.076 0.0060 5262.67 2.20 15.59
10 18.0 1.58 1.42 0.70 0.007 0.070 0.01 0.077 0.0031 6321.71 1.32 20.27
11 13.7 1.70 1.40 0.70 0.006 0.072 0.01 0.071 0.0027 6841.85 1.20 23.29
12 12.9 1.58 1.42 1.20 0.009 0.073 0.01 0.083 0.0054 6903.86 2.58 19.60
13 14.3 1.76 1.32 1.00 0.007 0.096 0.01 0.065 0.0033 7030.57 1.58 21.51
14 18.8 1.63 1.42 1.60 0.010 0.056 0.01 0.079 0.0067 11017.15 5.24 24.57
15 17.2 2.02 1.36 1.60 0.008 0.077 0.01 0.087 0.0042 13785.34 3.94 30.61
16 22.2 2.81 1.74 1.00 0.005 0.092 0.01 0.062 0.0017 20620.19 2.27 45.51
17 50.3 2.71 1.82 1.00 0.006 0.084 0.01 0.068 0.0019 30078.49 3.76 43.62
实测资料对其中的系数、指数进行了率定,在不少情况下,
公式计算值仍可能使计算从数值上接近含沙量,提高公式整
体的计算精度,但认真分析,阻力系数的错误贡献使公式计
算结果却出现违背冲积河流的河床和水流自动调整作用原理
的概念性错误。
费祥俊公式存在的问题还有 4个方面:第一,式(21)在
含沙量接近 0时等号右边会接近于 0,而等号左边一般水流
条件下并不为 0,说明该式存在一定的问题。第二,式(22)
采用 d 代表泥沙组成上限粒径,该粒径在悬移质泥沙级配中
90
颇为困难,
对应的含量很少,确定的 d 及其相应的沉速 ω 90
90
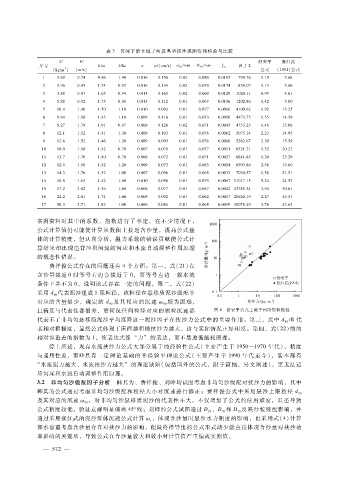
且精度与代表性都很差,更何况任何粒径对应的颗粒沉速都 图 4 舒安平公式土城子河段资料检验
代表不了非均匀悬移质泥沙平均沉降这一泥沙因子在挟沙力公式中的重要作用。第三,式中 d ?R代
90
表相对粗糙度,显然公式体现了床面越粗糙挟沙力越大,这与实际情况正好相反。第四,式( 22)前的
相对容重差的指数为 1,使表达式像 “力” 的表达,而不易遵循能耗原理。
综上所述,现有水流挟沙力公式大部分属于纯经验性公式(主要产生于 1950—1970年代),精度
与通用性差,那些具有一定理论基础的半经验半理论公式 (主要产生于 1990年代至今),基本都有
“水流阻力越大、水流挟沙力越大” 的理论缺陷(包括国外的公式,限于篇幅,另文阐述),更无法适
应河床和水流自动调整作用原理。
3.2 非均匀沙级配因子分析 韩其为、费祥俊、刘峰均试图考虑非均匀沙级配对挟沙力的影响,其中
韩其为公式通过考虑非均匀沙级配和粒径大小对沉速进行修正;费祥俊公式中采用悬沙上限粒径 d
90
,对非均匀沙悬移质泥沙的代表性不大,不仅增加了公式的使用难度,且还导致
及其对应的沉速 ω 90
公式精度较低,验证点群明显偏离 45°线;刘峰的公式试图通过 D 、D 和 D 反映沙粒级配影响,并
75
25
50
,体现含沙量时悬沙水力粗度的影响,也采用式(4)计算
通过采用张红武的泥沙群体沉速公式计算 ω s
浑水容重考虑含沙量存在对挟沙力的影响,但最终推导出的公式形式缺少能直接体现含沙量对挟沙效
率影响的关键项,导致公式在含沙量较大和较小时计算值严重偏离实测值。
— 5 7 —
2