Page 66 - 2023年第54卷第5期

１ ｎ ｓ
ｉ
ｂ＝ ∑ （２５）
ｋ
ｎ ｉ ＝１ ｓ
ｉ
１ ｎ ｓ － ｓ
ｉ
ｉ
ｂ＝ ∑ （２６）
ｐ
ｎ ｉ ＝１ （ｓ ＋ ｓ）?２
ｉ ｉ
２．２ 图示验证法 式（１）与式（６）均为适用于一般挟沙水流的挟沙力公式，可采用黄河水利委员会
１９５０年代历经两年在黄河土城子河段精心观测的资料 ［２９］ 进行验证（见图 １）。

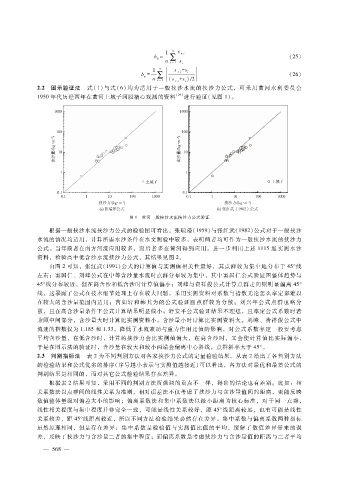
图 １ 黄河一般挟沙水流挟沙力公式验证

根据一般挟沙水流挟沙力公式的检验图可看出，张瑞瑾（１９５９）与张红武（１９８２）公式对于一般挟沙
水流的情况均适用，计算所需水沙条件在水文测验中较多，表明两者均可作为一般挟沙水流的挟沙力
公式。当年前者在南方河流应用较多，而后者多在黄河得到应用。进一步利用上述 １１１５组实测水沙
资料，检验高中低含沙水流挟沙力公式，其结果见图 ２。
由图 ２可知，张红武（１９９１）公式的计算值与实测值相关性最好，其点群较为集中地分布于 ４５°线
左右；窦国仁、刘峰公式在中等含沙量水流时点群分布较为集中，其中窦国仁公式验证图整体趋势与
４５°线分布较近，但在高含沙和低含沙时计算值偏小；刘峰与费祥俊公式计算点群走向则明显偏离 ４５°
线，这暴露了公式在技术细节处理上存在较大问题，采用实测资料对系数与指数无论怎么率定都难以
在较大的含沙量范围内适用；曹如轩和韩其为的公式验证图点群较为分散；刘兴年公式点群也略分
散，且在高含沙量条件下公式计算结果明显偏小；舒安平公式验证结果不理想，且率定公式系数时若
兼顾中间部分，含沙量大时计算比实测资料小，含沙量小时计算比实测资料大。刘峰、费祥俊公式中
流速的指数仅为 １．１８５和 １．３３，降低了水流紊动与重力作用比值的影响，对公式系数率定一般要考虑
平均含沙量，在低含沙时，计算的挟沙力会比实测值偏大，在高含沙时，又会使计算值比实际偏小，
于是在图示法的验证时，含沙量在较大和较小两端会偏离中心斜线，点群斜率大于 ４５°。
２．３ 判别指标法 表 ２为不同判别方法对各家挟沙力公式的定量检验结果。从表 ２给出了各判别方法
的检验结果和公式优劣的排序（序号越小表示与实测值越接近）可以看出，各方法对最优和最差公式的
判别结果是相同的，而对其它公式检验结果存在差异。
根据表 ２结果可知，采用不同的判别方法所强调的重点不一样，得出的结论也有差别。比如：相
关系数法以点群间的线性关系为准则，相对误差法不仅考虑了挟沙力与含沙量值间的距离，更能反映
数值整体量级对偏差大小的影响；偏离系数法和集中系数法以最小距离为核心标准，对于同一点群，
线性相关程度与集中程度并非完全一致，可能是线性关系较好，距 ４５°线距离较远，也有可能是线性
关系较差，距 ４５°线距离较近，所以不同方法检验结果必然存在差异。集中系数与偏离系数两种指标
虽然原理相同，但是存在差异：集中系数是检验值与实测值比值的平均，缓解了数值差异带来的误
差，反映了挟沙力与含沙量二者的集中程度；而偏离系数是考虑挟沙力与含沙量值的距离与二者平均

８
— ５ ６ —