Page 68 - 2023年第54卷第5期
P. 68
表 2 各水流挟沙力公式检验结果
检验方法 (1) (2) (3) (4) (5) (6) (7) (8)
0.86 0.76 0.75 0.72 0.60 0.60 0.58 0.54
相关系数法
张红武(1991) 舒安平 窦国仁 刘兴年 曹如轩 刘峰 韩其为 费祥俊
0.38 0.52 0.60 0.93 0.97 1.51 2.55 5.75
相对误差法
张红武(1991) 刘兴年 窦国仁 舒安平 韩其为 曹如轩 刘峰 费祥俊
0.96 1.05 0.86 0.67 1.58 2.21 3.37 6.47
集中系数法
张红武(1991) 舒安平 刘兴年 窦国仁 韩其为 曹如轩 刘峰 费祥俊
0.40 0.62 0.67 0.76 0.77 0.83 0.94 1.02
偏离系数法
张红武(1991) 刘兴年 韩其为 窦国仁 曹如轩 舒安平 刘峰 费祥俊
此外,图示法的直观判别结果与根据检验方法得到的结果也存在一定差异。如图 2(c)中,点群分
布在头尾两处均偏于对角线之上,仅由图而言,可认为公式较差,但是其计算的相关系数乃至相对误
差指标却较好,主要是因为,相关性仅反映点群的线性规律,与对角线的偏离程度无关;再如图 2(f)
中,刘兴年公式点群分布趋势明显偏离 45°线,但该公式集中系数表现较好,说明点群有可能在 50°~
60° 线附近有较强的集中分布。由此可见:对于水流挟沙力公式的检验,在考虑指标判别的同时,必
须重视公式的图示检验效果。
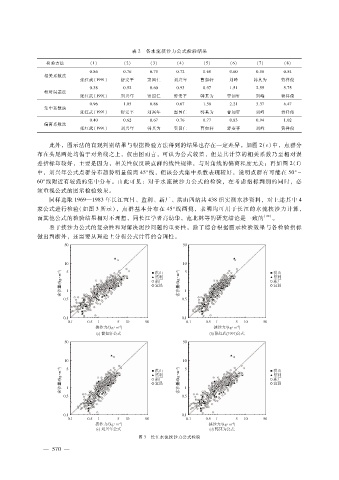
同样选取 1969—1983年长江宜昌、监利、新厂、洪山四站共 438组实测水沙资料,对上述其中 4
家公式进行检验(如图 3所示),点群基本分布在 45°线两侧,表明均可用于长江的水流挟沙力计算,
而其他公式的检验结果相对不理想,同长江学者高幼华,范北林等的研究结论是一致的 [28] 。
鉴于挟沙力公式的复杂性和对解决泥沙问题的重要性,除了综合根据图示检验效果与各检验指标
做出判断外,还需要从理论上分析公式计算的合理性。
图 3 长江水流挟沙力公式检验
— 5 7 —
0