Page 64 - 2023年第54卷第6期

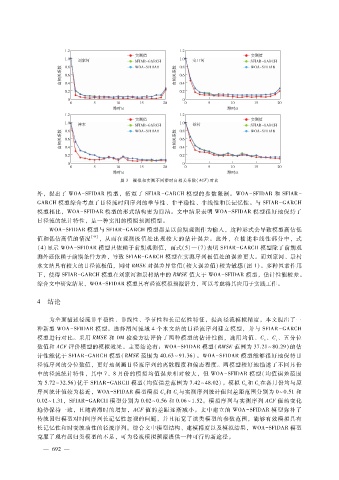
图 ３ 模拟和实测不同滞时自相关系数（ＡＣＦ）对比

外，提出了 ＷＯＡ － ＳＦＩＤＡＲ模型，拓宽了 ＳＦＩＡＲ － ＧＡＲＣＨ模型的参数限制。ＷＯＡ － ＳＦＩＤＡＲ和 ＳＦＩＡＲ －
ＧＡＲＣＨ模型综合考虑了日径流时间序列的季节性、非平稳性、非线性和长记忆性。与 ＳＦＩＡＲ － ＧＡＲＣＨ
模型相比，ＷＯＡ － ＳＦＩＤＡＲ模型的形式结构更为简洁。文中结果表明 ＷＯＡ － ＳＦＩＤＡＲ模型很好地保持了
日径流的统计特性，是一种实用的模拟预测模型。
ＷＯＡ － ＳＦＩＤＡＲ模型与 ＳＦＩＡＲ － ＧＡＲＣＨ模型都是以前期观测作为输入，这种形式会导致模型高估低
值和低估高值的情况 ［４４］ ，从而在观测极值处出现较大的估计误差。此外，在描述非线性部分中，式
（４）显示 ＷＯＡ － ＳＦＩＤＡＲ模型只依赖于前期观测值，而式（５）—（７）表明 ＳＦＩＡＲ － ＧＡＲＣＨ模型除了前期观
测外还依赖于前期条件方差，导致 ＳＦＩＡＲ － ＧＡＲＣＨ模型在实测序列极值处的误差更大。而刘家河、景村
水文站具有较大的日径流极值，同时 ＲＭＳＥ对误差异常值（较大误差值）较为敏感（图 １）。多种因素作用
下，使得 ＳＦＩＡＲ － ＧＡＲＣＨ模型在刘家河和景村站中的 ＲＭＳＥ值大于 ＷＯＡ － ＳＦＩＤＡＲ模型，估计性能较差。
综合文中研究结果，ＷＯＡ － ＳＦＩＤＡＲ模型具有径流模拟预报潜力，可以考虑将其应用于实践工作。

４ 结论

为全面描述径流非平稳性、非线性、季节性和长记忆性特征，提高径流模拟精度，本文提出了一
种新型 ＷＯＡ － ＳＦＩＤＡＲ模型。选择渭河流域 ４个水文站的日径流序列建立模型，并与 ＳＦＩＡＲ － ＧＡＲＣＨ
模型进行对比。采用 ＲＭＳＥ和 ＤＭ检验方法评价了两种模型的估计性能，选用均值、Ｃ、Ｃ、五分位
ｖ ｓ
数值和 ＡＣＦ评价模型的模拟效果。主要结论有：ＷＯＡ － ＳＦＩＤＡＲ模型（ＲＭＳＥ范围为 ３７．２１～８０．２９）的估
计性能优于 ＳＦＩＡＲ － ＧＡＲＣＨ模型（ＲＭＳＥ范围为 ４０．６３～９１．３６）。ＷＯＡ － ＳＦＩＤＡＲ模型能够很好地保持日
径流序列的分位数值，更好地刻画日径流序列的离散程度和偏态程度。两模型较好地描述了不同月份
中的径流统计特性，其中 ７、８月份的模拟均值误差相对较大，但 ＷＯＡ － ＳＦＩＤＡＲ模型（均值误差范围
为 ５．７２～３２．５６）优于 ＳＦＩＡＲ － ＧＡＲＣＨ模型（均值误差范围为 ７．４２～４８．０２）。模拟 Ｃ和 Ｃ在各月份均与原
ｖ ｓ
序列统计值较为接近，ＷＯＡ － ＳＦＩＤＡＲ模型模拟 Ｃ和 Ｃ与实测序列统计值间差距范围分别为 ０～０．５１和
ｓ
ｖ
０．０２～１．３１，ＳＦＩＡＲ － ＧＡＲＣＨ模型分别为 ０．０２～０．５６和 ０．０６～１．５２。模拟序列与实测序列 ＡＣＦ值的变化
趋势保持一致，且随着滞时的增加，ＡＣＦ值的差距逐渐减小。文中建立的 ＷＯＡ － ＳＦＩＤＡＲ模型弥补了
传统回归模型对时间序列长记忆性忽视的问题，并且拓宽了该类模型的参数范围，能够有效模拟具有
长记忆性和时变波动性的径流序列。综合文中模型结构、建模精度以及模拟结果，ＷＯＡ － ＳＦＩＤＡＲ模型
克服了现有回归类模型的不足，可为径流模拟预报提供一种可行的新途径。

— ６ ９ —
２