Page 15 - 2024年第55卷第8期

表 ３ 工程应用数值模型
模型 基体材料 网格布 初始缺陷 缺陷位置
模型 １ 聚脲材料 无 无
模型 ２ 聚脲材料 有 无
模型 ３ 聚脲材料 无 有 涂层底部
模型 ４ 聚脲材料 有 有 涂层底部
模型 ５ 聚氨酯材料 Ａ 无 有 涂层底部
模型 ６ 聚氨酯材料 Ａ 有 有 涂层底部
模型 ７ 聚氨酯材料 Ｂ 无 有 涂层底部
模型 ８ 聚氨酯材料 Ｂ 有 有 涂层底部
模型 ９ 聚脲材料 有 有 涂层中部
模型 １０ 聚脲材料 有 有 涂层顶部

９、１０用于对比验证当初始缺陷位置不同时，工程应用模型的计算结果差别，从而进一步验证模型的
有效性。
以模型 ４为例，涂层底部设置宽度× 深度为 ０．１ｍｍ × ０．３ｍｍ的初始缺陷，混凝土基面同聚脲涂层之间
［１８］
设置内聚力单元（ＣＯＨ２Ｄ４） ［２８］ 模拟粘接层，内聚力单元法向及切向粘接强度分别为 ２．５和 ３．２ＭＰａ 。
模型右侧混凝土固定，左侧混凝土施加向左的匀速水平位移边界条件，模拟基面开裂对顶部涂层的影
响，直至模型发生剥离破坏或涂层断裂破坏。采用二维平面应变单元（ ＣＰＥ４Ｒ）模拟混凝土基面、聚脲
材料及网格布纤维。整体模型共计结点数为 ９５０６，单元数为 ９０４０。该模型同时考虑材料非线性、几何
－ ５
非线性和材料破坏演化过程，同样需采用显示求解器求解，且计算步长不高于 １０ ｓ。其他模型设置
同模型 ４类似，不再赘述。
５．２ 基体材料为聚脲 对比模型 １、２，以及模型 ３、４计算结果，考察设置网格布同不设置网格布的
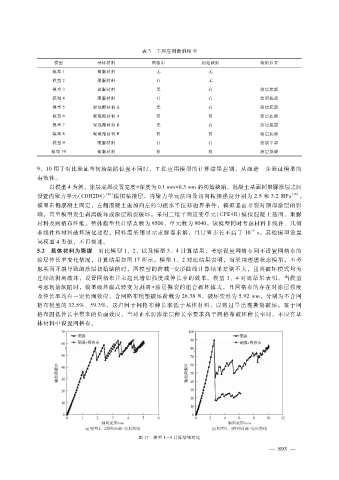
涂层伸长率变化情况，计算结果如图 １７所示。模型 １、２对比结果表明，当采用理想状态模型，不考
虑基面开裂导致的涂层初始缺陷时，两模型的荷载 － 变形曲线计算结果差别不大，且其破坏模式均为
连续的剥离破坏，设置网格布并未起到增加强度或伸长率的效果。模型 ３、４对比结果表明，当模型
考虑初始缺陷时，模型破坏模式转变为剥离 ＋ 涂层撕裂的组合破坏模式，且网格布的存在对涂层强度
及伸长率均有一定负面效应，含网格布模型破坏荷载为 ２６．３８Ｎ，破坏变形为 ５．９２ｍｍ，分别为不含网
格布模型的 ３２．５％、５９．３％，这归因于网格布伸长率低于基体材料，以致过早出现撕裂破坏。鉴于网
格布因低伸长率带来的负面效应，当对止水防渗涂层伸长率要求高于网格布破坏伸长率时，不应在基
体材料中设置网格布。

图 １７ 模型 １—４计算结果对比
— ８ ９ ３ —