Page 10 - 2024年第55卷第8期

采用线弹性本构模型模拟聚酯纤维，弹性模量可基于试验数据通过最小二乘法拟合获得，此处取
值为 ４５．５ＭＰａ，泊松比为 ０．１５，破坏应变为 ０．４０５。建立方格网眼（如图 １所示）网格布数值模型以验
证材料本构模型的可靠性，模型几何尺寸如图 ６（ａ）所示，整体模型长度 × 宽度为 ２００ｍｍ × ５０ｍｍ。为
减少计算量，采用半模型建模，剖面施加对称约束，模型底端固定，顶端加载方式为位移加载，以匀
速施加轴向拉伸位移直至模型发生断裂破坏。
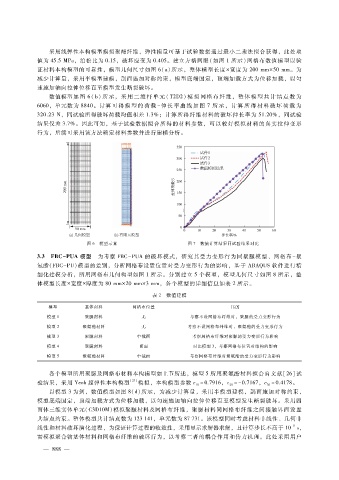
数值模型如 图 ６（ｂ）所 示，采 用 二 维 杆 单 元 （Ｔ２Ｄ２）模 拟 网 格 布 纤 维，整 体 模 型 共 计 结 点 数 为
６０６０，单元数为 ８８４０。计算 可 得 模 型 的 荷 载 － 伸 长 率 曲 线 如 图 ７所 示， 计 算 所 得 材 料 破 坏 荷 载 为
３２０．２３Ｎ，同试验所得破坏荷载均值相差 １．３％；计算所得纤维材料的破坏伸长率为 ５１．２０％，同试验
结果仅差 ３．７％。因此可知，基于试验数据拟合所得的材料参数，可以较好模拟材料的真实拉伸变形
行为，后续可采用该方法确定材料参数并进行建模分析。

图 ６ 模型示意 图 ７ 数值计算结果同试验结果对比

３．３ ＦＢＣ － ＰＵＡ模型 为考察 ＦＢＣ － ＰＵＡ的破坏模式，研究其受力变形行为同聚脲模型、网格布 － 聚
氨酯（ＦＢＣ － ＰＵ）模型的差别，分析网格布设置位置对受力变形行为的影响，基于 ＡＢＡＱＵＳ软件进行精
细化建模分析，所用网格布几何构型如图 １所示。分别建立 ５个模型，模型几何尺寸如图 ８所示，整
体模型长度× 宽度× 厚度为 ８０ｍｍ × ２０ｍｍ × ３ｍｍ，各个模型的详细信息如表 ２所示。
表 ２ 数值建模

模型 基体材料 网格布位置 目的
模型 １ 聚脲材料 无 考察不设网格布纤维时，聚脲的受力变形行为
模型 ２ 聚氨酯材料 无 考察不设网格布纤维时，聚氨酯的受力变形行为
模型 ３ 聚脲材料 中截面 考察网格布纤维对聚脲的受力变形行为影响

模型 ４ 聚脲材料 顶面 对比模型 ３，考察网格布位置对结构的影响
模型 ５ 聚氨酯材料 中截面 考察网格布纤维对聚氨酯的受力变形行为影响

各个模型所用聚脲及网格布材料本构模型如上节所述，模型 ５所用聚氨酯材料拟合自文献［２６］试
验结果，采用 Ｙｅｏｈ超弹性本构模型 ［２７］ 模拟，本构模型参数 ｃ ＝ ０ ．７９１６，ｃ ＝－ ０ ．７１６７，ｃ ＝ ０ ．４１７８。
３０
１０
２０
以模型 ３为例，数值模型如图 ８（ｄ）所示，为减少计算量，采用半模型建模，剖面施加对称约束，
模型底端固定，顶端加载方式为位移加载，以匀速施加轴向拉伸位移直至模型发生断裂破坏。采用四
面体三维实体单元（Ｃ３Ｄ１０Ｍ）模拟聚脲材料及网格布纤维，聚脲材料同网格布纤维之间接触界面设置
共结点约束。整体模型共计结点数为 １２３１４１，单元数为 ８７７３１。该模型同时考虑材料非线性、几何非
－ ５
线性和材料破坏演化过程，为保证计算过程的收敛性，采用显示求解器求解，且计算步长不高于 １０ ｓ，
需模拟聚合物基体材料和网格布纤维的破坏行为，以考察二者的耦合作用和传力机理。此处采用用户

— ８ ８ —
８