Page 12 - 2024年第55卷第8期

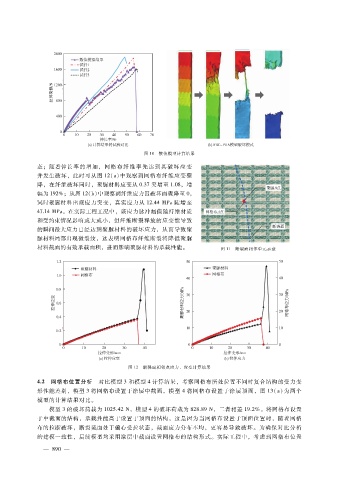
图 １０ 数值模型计算结果

态；随着伸长率的增加，网格布纤维率先达到其破坏应变
并发生破坏，此时可从图 １２（ａ）中观察到网格布纤维应变骤
降，在纤维破坏同时，聚脲材料应变从 ０．３７突增至 １．０８，增
幅为 １９２％；从图 １２（ｂ）中观察到纤维应力因破坏而骤降至 ０，
同时聚脲材料出现应力突变，真实应力从 １２．４４ＭＰａ陡增至
４７．１４ＭＰａ。在实际工程工况中，该应力脉冲幅值随纤维材质
和受约束情况影响或大或小，但纤维断裂释放的应变能导致
的瞬间最大应力已经达到聚脲材料的破坏应力，从而导致聚
脲材料局部出现微裂纹，这表明网格布纤维断裂将降低聚脲
材料截面的有效承载面积，进而影响聚脲材料的承载性能。 图 １１ 断裂面相邻单元示意

图 １２ 断裂面相邻点应力、应变计算结果

４．２ 网格布位置分析 对比模型 ３和模型 ４计算结果，考察网格布所处位置不同时复合结构的受力变
形性能差别，模型 ３将网格布设置于涂层中截面，模型 ４将网格布设置于涂层顶面，图 １３（ａ）为两个
模型的计算结果对比。
模型 ３的破坏荷载为 １０２５．４２Ｎ，模型 ４的破坏荷载为 ８２８．８９Ｎ，二者相差 １９．２％。将网格布设置
于中截面的结构，承载性能高于设置于顶面的结构，这是因为当网格布设置于顶面位置时，随着网格
布的拉断破坏，断裂截面处于偏心受拉状态，截面应力分布不均，更容易导致破坏。为确保对比分析
的建模一致性，后续模型均采用涂层中截面设置网格布的结构形式。实际工程中，考虑到网格布位置

— ８ ９ —
０