Page 9 - 2024年第55卷第8期

ｎ ２ μ ｉ
∑
Ｐ ＝ ( （ λ － α ｉ ?２ － λ － α ｉ ?４ ） ) （７）
ｉ ＝１ α ｉ
代入式（ ６）可得：
ｎ
σ １１ ∑ ( ２ μ ｉ （ λ － ２ λ － α ｉ ?２ ＋ λ － α ｉ ?４ ） ) （８）
＝
α ｉ
ｉ ＝１ α ｉ
为需要拟合的 Ｏｇｄｅｎ模型参数。
式中 μ ｉ 、α ｉ
目前主流的商用有限元软件，如 ＡＢＡＱＵＳ等均内置了 Ｏｇｄｅｎ超弹性本构模型，上述非线性黏弹性
材料本构模型的应用较为便捷可靠。综合考虑收敛性和准确性，此处采用二阶 Ｏｇｄｅｎ模型，根据试验
结果拟合所得材料本构模型参数如表 １所示。
表 １ 聚脲材料本构参数

项目 材料参数
＝
＝
＝
Ｏｇｄｅｎ模型参数?ＭＰａ μ １ ０ ．０１０７，α １ ７ ．９５９，μ ２ １３ ．５５８，α ２ ＝－ ２ ．７５３
－ ２
－ ７
－ ６
－ ４
－ ３
－ ５
＝
＝
＝
＝
＝
＝
τ １ ２ ．０ × １０ ，τ ２ ２ ．０ × １０ ，τ ３ ２ ．０ × １０ ，τ ４ ２ ．０ × １０ ，τ ５ ２ ．０ × １０ ，τ ６ ２ ．０ × １０ ，
＝
＝
τ ７ ０ ．２，τ ８ ２ ，τ ９ ２０ ，τ １０ ２００ ，
＝
＝
Ｐｒｏｎｙ 序列参数
＝
＝
＝
＝
＝
＝
＝
ｇ １ ０．１１５７，ｇ ２ ０．１５３３，ｇ ３ ０．１７０３，ｇ ４ ０．１５８５，ｇ ５ ０．１２３７，ｇ ６ ０．０８０９，ｇ ７ ０．０４４４，
＝
＝
ｇ ８ ０ ．０２０４，ｇ ９ ０ ．００７９，ｇ １０ ０ ．００２５
＝
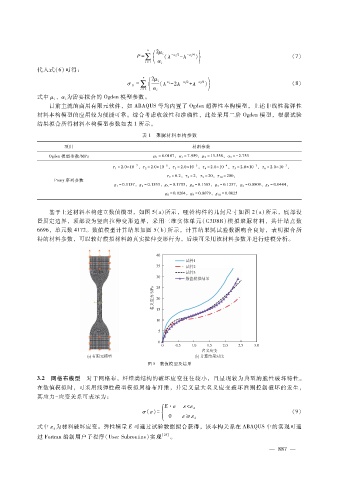
基于上述材料本构建立数值模型，如图 ５（ａ）所示，哑铃构件的几何尺寸如图 ２（ａ）所示，底部设
置固定边界，顶部设为竖向拉伸变形边界，采用三维实体单元（ Ｃ３Ｄ８Ｒ）模拟聚脲材料，共计结点数
６６９６，单元数 ４１７２。数值模型计算结果如图 ５（ｂ）所示，计算结果同试验数据吻合良好，表明拟合所
得的材料参数，可以较好模拟材料的真实拉伸变形行为，后续可采用该材料参数并进行建模分析。

图 ５ 数值模型及结果

３．２ 网格布模型 对于网格布，纤维类结构的破坏应变往往较小，且呈现较为典型的脆性破坏特性。
在数值模拟时，可采用线弹性模型模拟网格布纤维，并定义最大名义应变破坏准则控制破坏的发生，
其应力－ 应变关系可表示为：

Ｅ·ε ε ＜ ε ｄ
σ （ ε ） ＝ ０ { ε≥ε ｄ （９）

为材料破坏应变。弹性模量 Ｅ可通过试验数据拟合获得，该本构关系在 ＡＢＡＱＵＳ中的实现可通
式中 ε ｄ
过 Ｆｏｒｔｒａｎ编制用户子程序（ＵｓｅｒＳｕｂｒｏｕｔｉｎｅ）实现 ［２５］ 。

— ８ ８ ７ —